論文読み 2015, Simultaneous Deep Transfer Across Domains and Tasks

元ネタ: Tzeng and Saenko, Simultaneous Deep Transfer Across Domains and Tasks, 2015, ICCV 2015

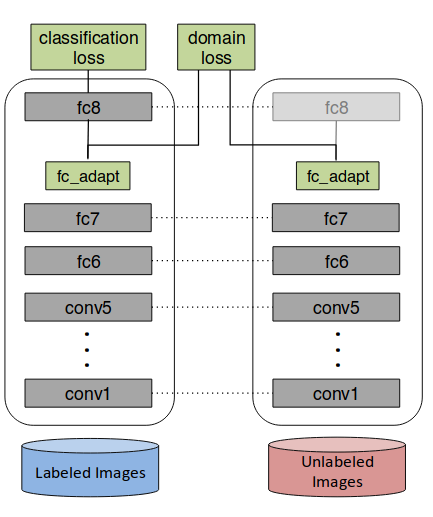
figure 1. Deep Domain Confusionのダイアグラム

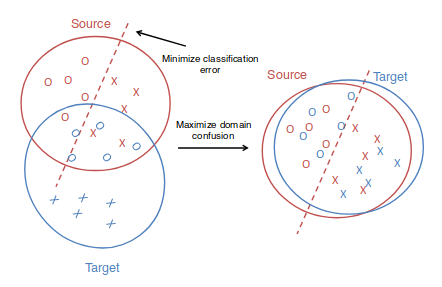
Tzengの前の論文では，source domain での分類と並行して，sourceとtargetに対して生成する表現が似てくるように学習させるため，confusion loss
$MMD(X_s, X_T) = \left\| \frac{1}{|X_s|}\sum_{x_S \in X_S} \phi(x_s) - \frac{1}{X_T} \sum_{x_t \in X_T} \phi(x_t)\right\|$
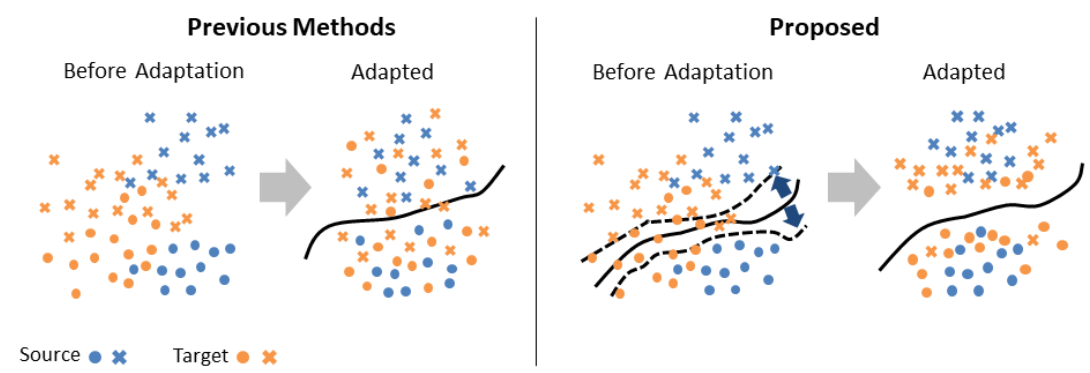
をも最適化するように学習させた(fig.1)．しかしdomain同士の表現が似ていてもそれぞれの内部でdecision boundaryが似ているかは別の話だから，この論文では表現の構造のみならずsource domainのラベルの構造をtarget domainに変換する．変換にはtarget domainにいくつかラベル付きの点が必要だから，unsupervised domain adaptationに直接適用することはできない．

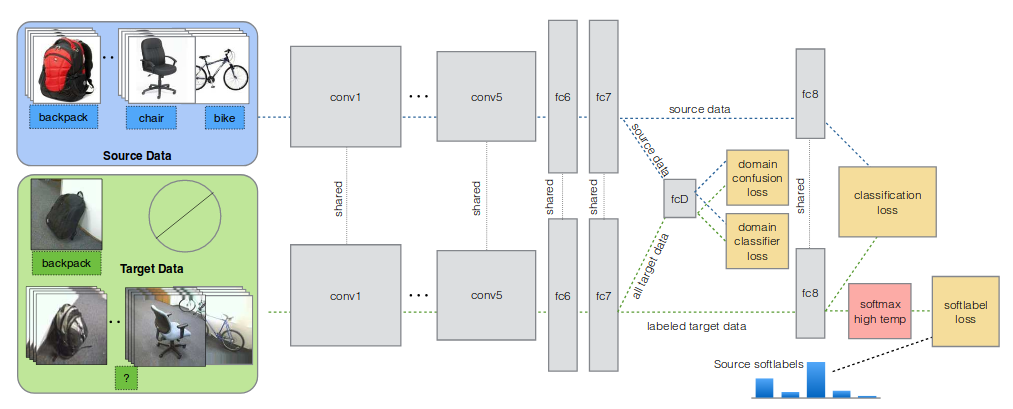
figure 2. Simultaneous Deep Transferのダイアグラム

domain confusionによって表現を似せる

インプットからfc7までを，表現を生成するネットワークGとし，Gの出力する表現$\theta_{\text{repr}}$がsource domainから来たのかtarget domainから来たのか区別するネットワークfcDを構成する．fcDは通常のnegative log likelihoodによって最適化する．つまり損失関数は
$\mathcal{L}_D(x_S, x_T, \theta_{\text{repr}}; \theta_D) = -\sum_{d \in \{\text{source, target}\}} 1_{[y_D = d]} \log q_d$
ただし$\theta_D$はfcDの重みで，$q_d$はfcDの結果のlogit．

さらにfcDを騙すようにGを最適化する(adversarial learning)．損失関数は
$\mathcal{L}_{\text{conf}}(x_S, x_T, \theta_D; \theta_{\text{repr}} = - \sum_{d} \frac{1}{D} \log q_d$

sourceからtargetへのクラス構造のadaptation

通常ニューラルネットワークの(Kクラスの)クラス分類では，最終層にK個のニューロンを配置し，その出力にsoftmaxをかけてそのargmaxに対応するクラスをそのネットワークの推測とするわけだが，ここではsoftmaxの出力そのものに様々な操作を行っていく．
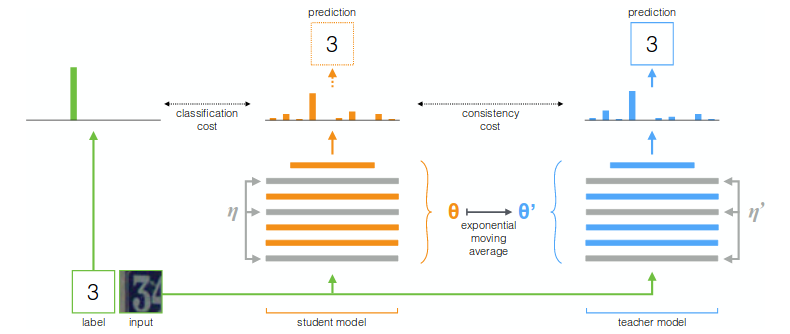
特に，あるクラスに対応するデータ点全てのsoftmaxの出力の平均を"soft label"と定義する(fig.3).ただし通常のsoftmaxはピークが強調されすぎるので，softmaxの温度$\tau$を高くする．
$\text{softmax}_{\tau}^{(k)}(\mathbf{x}) = \frac{\exp(\mathbf{x}_{(k)}/\tau)}{\sum_j\exp(\mathbf{x}_{(j)}/\tau)}$

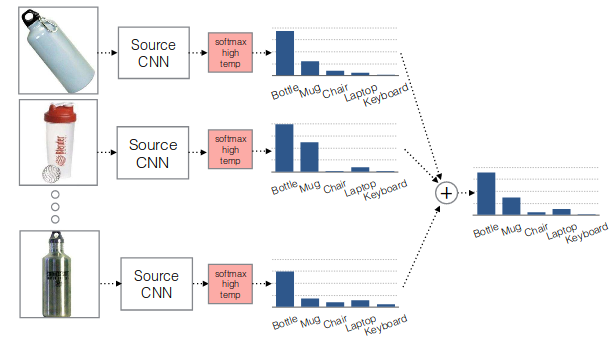
figure 3. soft label概念図

これによってsource domainにおける各くらすにおけるsoft labelが計算できる．これらのsoft labelに対して,ラベル付きのtarget domainの点$\{x_T, y_T\}$に対して損失関数を
$\mathcal{L}_{\text{soft}} (x_T, y_T;\theta_{\text{repr}},\theta_C)=-\sum_i l_i^{(y_T)}\log p_i$
とする.ただし$p$は$x_T$に対するsoft activation, $l_i$はsource domainのクラスiに対応するsoft label,
この損失というのはtargetのsoft activationとsourceのsoft labelの，targetクラスにおけるcross-entropyに等しい(fig.4).

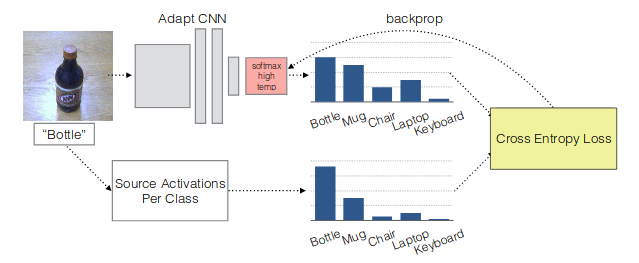
figure 4. soft loss

以上のlossを最適化する．

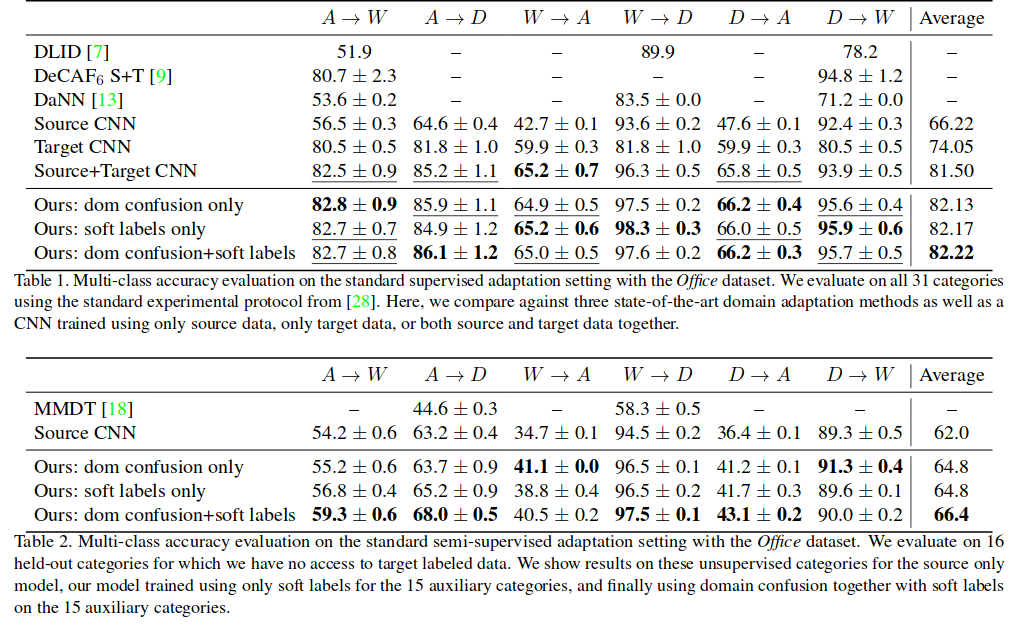
結果

論文読み 2014, Deep Domain Confusion: Maximizating for Domain Invariance

元ネタ: Tzeng et al. Deep Domain Confusion: Maximizing for Domain Invariance, 2014
図表は特に断りがない限りこの論文から引用

Domain adaptationのメソッド．ネットワークがsource domainとtarget domainに共通する表現を学習し，かつsource domainで優れた分類モデルとなるようにすれば，target domainにおいても優れた分類を行えるはずである(fig.1)．
そこで，source, target domainにおける表現$\phi$の距離をMaximum Mean Discrepancy(MMD)と定義しdomain (confusion) lossとよび，classification lossとの和を最適化する.$\phi$をネットワークとして

$MMD(X_s, X_T) = \left\| \frac{1}{|X_s|}\sum_{x_S \in X_S} \phi(x_s) - \frac{1}{X_T} \sum_{x_t \in X_T} \phi(x_t)\right\|$

figure 1. domain confusion概念図

Deep domain confusionでは，fc_adapt層以外のパラメータを共有するネットワークを2つ用意し，ラベルのついたデータ店に対してのみclassification loss を計算し，さらにすべてのデータ点でdomain lossを計算し，その和を最適化する．(fig.2)．
fc_adaptはそれぞれのネットワークで異なり，source domainとtarget domainの違いを吸収する．

figure 2. Deep Domain Confusion 概念図(破線はパラメータの共有を意味する)

このメソッドはadversarial learningとして見ることもできる(らしいSaito et al, 2017)．
conv1 - fc7をgenerator, fc_adaptをdiscriminator(critic), fc8をclassifierとして，discriminatorがsource domain, target domainを区別できないようにgeneratorを学習すると同時に，classifierが正しくクラス分類を行うように学習するのである(fc_adaptをdomain lossが大きくなるように学習していないのが気になるところだ).

論文読み 2017, Mean teachers are better role models: Wieght-averaged consistency targets improve semi-supervised deep learning results

元ネタ: Tarvainen and Valpola, Mean teachers are better role models: Weight-averaged consistency targets improve semi-supervised deep learning results, 2017
図表は特に断りがない限りこの論文から引用

Temporal Ensemblingでは，あるデータ点$x$に対して過去に計算した結果$z_1, ...z_k$のexponential moving average(EMA)を教師モデルの出力$\tilde{z}_{k+1}$としていた．この場合教師モデルが過去のエポック$(1, ...., k)$で決まるから，第$k+1$ エポックで学習してきた情報が教師モデルに統合されておらず，データセットが大きいほど学習のペースが遅くなってしまい，また過去のすべてのデータ点に対する出力を保持する必要がある．
そこで著者らは前のイテレーションにおけるネットワークの重みのEMAを教師モデルとする方法を考え，Mean Teacherと名付けた．

fig.1 Mean Teacherのダイアグラム

論文読み2018, ADVERSARIAL DROPOUT REGULARIZATION

元ネタ: Saito et al, Adversarial Dropout Rgeularization, 2018
図表は特に断りがない限りこの論文から引用

Adversarial Dropout Regularization(ADR)はDomain Adaptationの手法で，dropoutの場所だけが異なるネットワークの出力の差異が大きくなるデータ点がdecision boundaryに近いと考えて，ネットワークの出力がそのdecision boundaryから遠ざかるように最適化する．

• 従来手法(Tzeng et al. 2014, Ganin and Lempitsky, 2014)
  ネットワークをエンコーダー(generator)G, クラス分類器C, ドメイン分類器(Discriminator)Dに分けG->D->CかC<-G->Dの順に並べる.Eによって元の画像から生成された表現を，Dがsource domainに属するか，target domainに属するかを推測し，Gはその推測を間違わせるように最適化される．これによってGによる表現はsource, target domainにおいて共通となる．またsource domainのデータ点についてDが正しく分類できるようにDを最適化する．

従来手法ではDはドメインの違いしか考えていなかったので，Gがクラス分類に役に立たない表現にされてしまう(fig1, 左)．

本手法ではDを廃する．source domainではGとCは一連のclassification networkとして学習を行い，target domainではCはdecision boundaryに近いデータ点の検出器となって，GとCは敵対的に学習を行う．というのもCがクラス間のdecision boundaryに近い点に敏感なら,GはCを騙すためクラス間のdecision boundaryの近くにデータ点を写像するのをやめるはずで，したがってGはよりtarget domainでのクラス分類に役立つ表現を学習するようになる.(fig.1, 右)

figure 1. 従来手法と本手法の概念図

クラス間のdecision boundaryを決めているのはクラス分類器Cであって，Cのdropoutの場所を変えることで，Cが僅かに変化し，したがってdecision boundaryも僅かに変化する．decision bondaryの近くの点ほどこのdecision boundaryの変化によって大きくCの出力が変化する. この変化によってCはdecision boundaryに近いデータ点を検出する．
Cのdropoutの位置の異なった2つの現れをC1, C2として，データ点$x_t$に対するそれぞれの出力を$p_1, p_2$とする．その距離を
$d(p_1, p_2) = \frac{1}{2} (D_{KL}(p_1||p_2) + D_{KL} (p_2||p_1))$
と定める．

学習のプロセス

1. GとCは一連の分類器として学習する.最適化する対象は
   $\text{minimize}_{G, C} L(X_s, Y_s)$
   $L(X_s, Y_s) = -E_{\mathbf{x}_s, y_s} \sum_k 1_{k=y_s} \log p(y|\mathbf{x}_s)$
2. Cはdecision boundaryに近いtarget domainの点を検出するように学習する．また，1.ですでに行ったことだが，source domainでの分類器としても学習を行うと性能が向上した. 最適化する対象は
   $\text{minimize}_C\{ L(X_s, Y_s) - E_{\mathbf{x}_t \in X_t} [d(p_1, p_2)]\}$
3. Gがtarget domainでのCを騙すように最適化する．最適化する対象は
   $\text{minimize}_G\{ L_{adv}(X_t) + E_{\mathbf{x}_t \sim X_t} \sum_k p(y=k|\mathbf{x}_t) \log p (y|\mathbf{x}_t)\}$
   $L_{adv}(X_t)=E_{\mathbf{x}_t \sim X_t} [d(p_1, p_2)]$
   このステップは複数回行うと性能が向上する．