論文読み 2017, Temporal Ensembling for Semi-Supervised Learning manifold

元ネタ: Samuli Laine and Timo Aila, Temporal Ensembling for Semi-Supervised Learning, 2017, ICLR 2017
図表は特に断りがない限りこの論文から引用

複数のモデルのensembleは教師の有無にかかわらずよく使われる手法で，dropoutによる性能向上も内部で複数のモデルのensembleが起きているためだという人もいる．この論文ではdropout(とdata augmentation)によるensembleによって高精度な教師モデルを構成し，生徒モデルが教師モデルの出力を真似ることで半教師あり学習を行う．
Data Distillatinを思い出すが，Data Distillationは教師モデルがハードなラベル(すなわちクラスラベルそのもの)を推測してNLLやCrossEntropyをLossとして生徒モデルを最適化したのに対し，こちらでは同じ入力からの教師モデルと生徒モデルの出力の差異をLossとする. またラベル付きのデータ点に対してのみ，CrossEntropyをLossに足して最適化する．

dropoutの場所を変えてensembleを行う$\Pi$-modelと,過去のepochにおける出力とensembleを行うTemporal ensemblingが提案されている.

$\Pi$-model

同じexample $x$について，確率的なaugmentationやdropoutによってニューラルネットワーク$f_\theta$は非決定的な関数だから，$z=f_\theta(x), \tilde{z} = f_\theta(x)$は異なっているはずで，その差異$\|z - \tilde{z}\|$を小さくする．さらに$x$がラベル付きであるとき，$z, \tilde{z}$とそのラベルの乖離を小さくする．この場合，教師モデルと生徒モデルは同じものである．

fig.1 $\Pi$-modelのダイアグラム

fig.2 $\Pi$-modelのアルゴリズム

Temporal ensembling

$\Pi$-modelではネットワークのパラメータ$\theta$を変えずに$z, \tilde{z}$を計算したが，Temporal ensemblingでは過去のepochで計算した値のexponential moving averageを教師モデルの出力$\tilde{z}$とする．

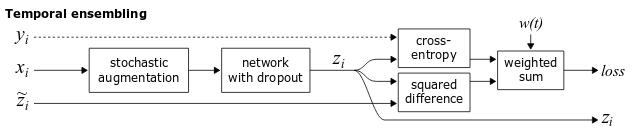
fig.3 Temporal Ensemblingのダイアグラム

fig.4 Temporal Ensemblingのアルゴリズム