論文読み2018, ADVERSARIAL DROPOUT REGULARIZATION

元ネタ: Saito et al, Adversarial Dropout Rgeularization, 2018
図表は特に断りがない限りこの論文から引用

Adversarial Dropout Regularization(ADR)はDomain Adaptationの手法で，dropoutの場所だけが異なるネットワークの出力の差異が大きくなるデータ点がdecision boundaryに近いと考えて，ネットワークの出力がそのdecision boundaryから遠ざかるように最適化する．

• 従来手法(Tzeng et al. 2014, Ganin and Lempitsky, 2014)
  ネットワークをエンコーダー(generator)G, クラス分類器C, ドメイン分類器(Discriminator)Dに分けG->D->CかC<-G->Dの順に並べる.Eによって元の画像から生成された表現を，Dがsource domainに属するか，target domainに属するかを推測し，Gはその推測を間違わせるように最適化される．これによってGによる表現はsource, target domainにおいて共通となる．またsource domainのデータ点についてDが正しく分類できるようにDを最適化する．

従来手法ではDはドメインの違いしか考えていなかったので，Gがクラス分類に役に立たない表現にされてしまう(fig1, 左)．

本手法ではDを廃する．source domainではGとCは一連のclassification networkとして学習を行い，target domainではCはdecision boundaryに近いデータ点の検出器となって，GとCは敵対的に学習を行う．というのもCがクラス間のdecision boundaryに近い点に敏感なら,GはCを騙すためクラス間のdecision boundaryの近くにデータ点を写像するのをやめるはずで，したがってGはよりtarget domainでのクラス分類に役立つ表現を学習するようになる.(fig.1, 右)

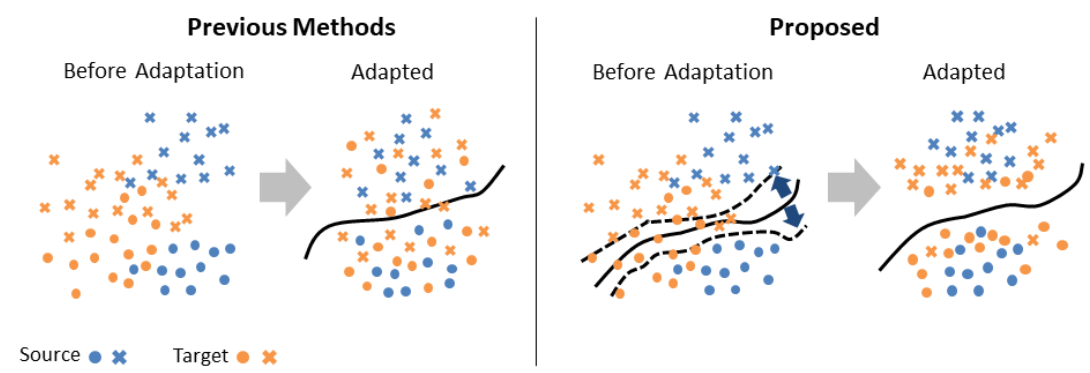
figure 1. 従来手法と本手法の概念図

クラス間のdecision boundaryを決めているのはクラス分類器Cであって，Cのdropoutの場所を変えることで，Cが僅かに変化し，したがってdecision boundaryも僅かに変化する．decision bondaryの近くの点ほどこのdecision boundaryの変化によって大きくCの出力が変化する. この変化によってCはdecision boundaryに近いデータ点を検出する．
Cのdropoutの位置の異なった2つの現れをC1, C2として，データ点$x_t$に対するそれぞれの出力を$p_1, p_2$とする．その距離を
$d(p_1, p_2) = \frac{1}{2} (D_{KL}(p_1||p_2) + D_{KL} (p_2||p_1))$
と定める．

学習のプロセス

1. GとCは一連の分類器として学習する.最適化する対象は
   $\text{minimize}_{G, C} L(X_s, Y_s)$
   $L(X_s, Y_s) = -E_{\mathbf{x}_s, y_s} \sum_k 1_{k=y_s} \log p(y|\mathbf{x}_s)$
2. Cはdecision boundaryに近いtarget domainの点を検出するように学習する．また，1.ですでに行ったことだが，source domainでの分類器としても学習を行うと性能が向上した. 最適化する対象は
   $\text{minimize}_C\{ L(X_s, Y_s) - E_{\mathbf{x}_t \in X_t} [d(p_1, p_2)]\}$
3. Gがtarget domainでのCを騙すように最適化する．最適化する対象は
   $\text{minimize}_G\{ L_{adv}(X_t) + E_{\mathbf{x}_t \sim X_t} \sum_k p(y=k|\mathbf{x}_t) \log p (y|\mathbf{x}_t)\}$
   $L_{adv}(X_t)=E_{\mathbf{x}_t \sim X_t} [d(p_1, p_2)]$
   このステップは複数回行うと性能が向上する．