オートエンコーダーによるクラスタリング

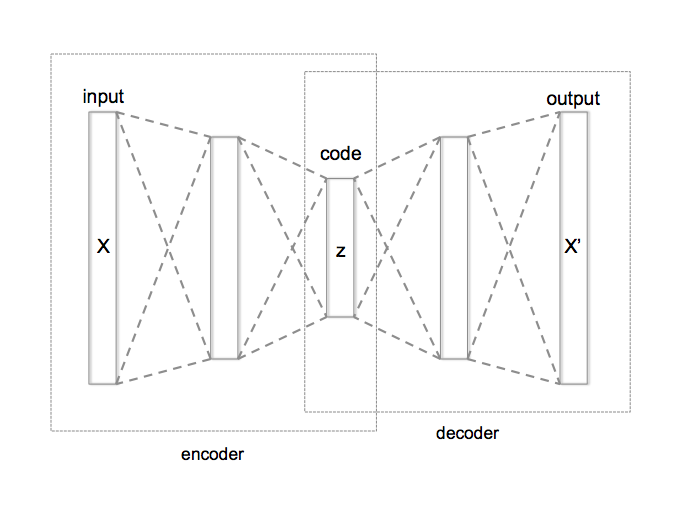
AutoEncoder(AE)は一般に砂時計の形をしたNNで,入力の次元よりも小さい次元に一旦情報を落とし込み(code),また元の次元の情報を再構成する.再構成された情報と元の入力の誤差によって学習を行うため,self-supervisedな学習と言われる.AEによる次元削減を利用してクラスタリングを行うことができる.もとのデータが高次元過ぎるとk-meansのような伝統的なクラスタリングアルゴリズムがうまく動かないので,低次元な空間に写してクラスタリングを行うのである.直感的には移した先の空間で従来のクラスタリングを行うのが簡単だが,アルゴリズムの途中でNNのパラメータを更新するアルゴリズムもある.今回はAEによるクラスタリングについての3本の論文を読む.
以下,データセットを\(\{x_1, ..., x_n\} = X \subset \mathbf{R}^{D_{X}}\)とし,AEによってそれぞれの元は\(\{z_1, ..., z_n\}=Z \subset \mathbf{R}^{D_{Z}}\)に写されるとし,その写像を\(\phi_W\)と書き,クラスターの数を\(K\)とする.

I. Unsupervised Deep Embedding for Clustering Analysis, 2016

1. parameter initialization

深いAEを学習させるため,すべての層を同時に学習させるのではなく,それぞれの層を取り出して隠れ層1のAEとして学習させ,あとで結合させる学習法をStacked AutoEncoder(SAE)という. この論文ではSAEによってfully connectedなAEを学習させて,\(\phi_W\)の初期値を決定している.
\(\{z_i\}_1^n = \{\phi_W(x_i)\}_1^n\)を得て,さらにk-meansで\(\{z_i\}\)のセントロイドの集合\(\{\mu_j\}_1^K\)を計算する.

2. optimization

(1) soft assignment

\(z_i\)がセントロイド\(\mu_j\)に属している確率\(q_{ij}\)をt分布によって以下のように計算する.(\(\alpha=1\)に統一)
\[q_{ij} = \frac{(1+\|z_i - \mu_j\|^2/\alpha)^{-\frac{\alpha + 1}{2}}}{\sum_{j'} (1+\|z_i - \mu_j'\|^2/\alpha)^{-\frac{\alpha + 1}{2}}}\]

(2) KL divergence minimization

auxiliary target distribution \(P\)を導入する. \(P\)は真の分布に近いと仮定されており,本アルゴリズムがやることはsoft assignmentと\(P\)を合致させることであって,そのために,soft assignment \(Q\)と\(P\)のKL divergenceを目的関数として最小化する:
\[L = D_{KL}(P||Q) = \sum_i \sum_j p_{ij} \log \frac{p_{ij}}{q_{ij}}\]
\(P\)の選び方は難しい問題で,論文内では
\[p_{ij} = \frac{q^2_{ij} / f_j}{\sum_{j'} q^2_{ij'} / f_j'}, \ f_j = \sum_i q_{ij}\text{ (soft cluster frequency)}\]
としている…
\[\frac{\partial L}{\partial z_i} = \frac{\alpha + 1}{\alpha} \sum_j \left(1 + \frac{\|z_i - \mu_j\|^2}{\alpha} \right)^{-1}\]
\[\frac{\partial L}{ \partial \mu_j } =-\frac{\alpha + 1}{\alpha} \sum_i \left(1 + \frac{\|z_i - \mu_j\|^2}{\alpha} \right)^{-1} \times (p_{ij}-q_{ij})(z_i-\mu_j)\]
が成立し,これをNNに渡してbackpropagationすることでNNをも同時に更新でき,新しい\(Z\)の点\(\{z_i\}\)とセントロイド\(\{\mu_j\}\)が計算できる. NNを更新しない場合.つまり\(\{\mu_j\}\)だけを更新する場合,NNを更新する場合よりも性能が下回る.
データ点のクラスター間の変動が,総データ数\(n\)の\(tol\) %を下回ったら計算を打ち切る.

II. Deep Clustering with Convolutional Autoencoders, 2017

Iの自然な拡張. AEをCovolutional AutoEncoderに変更し,空間的な情報をより活用できるとしている. Poolingではなくstrided convolutionによってencodeし,strided transposed convolutionによってdecodeしている.

また,I.ではdecoder部分は削除していたが,この論文では残し,objective functionにreconstruction lossを加えて,code部分が空間情報を再構成するための情報を保存するようにしているこれによって,単にAEをCAEに変えただけの場合よりも性能が向上している.

III Deep Clustering via Joint Convolutional Autoencoder Embedding and Relative Entropy Minimization

(I, IIと揃えるため,auxiliary distributionをP, それに近づけていくモデル分布をQとする)
このアルゴリズムはモデルの分布\(Q\)に近く,事前分布を満足する\(P\)を推定(expectation step)してから,\(P\)に近づくようにモデル分布\(Q\)を更新する(maximization step).
\(\mathbf{R}^{d_Z}\)を\(\mathbf{R}^K\)に移す写像\(f_\theta\)を
\[f_\theta(z) = \frac{\exp(\theta^T_k z_i)}{\sum_{k'} \exp(\theta^T_{k'} z_i)}\]
と定める.このとき,\(x_i\)がクラスター\(j\)に属する確率を\(f_\theta(z_i)\)とする.つまり
\[q_{ij} = P(y_i = j| z_i, \theta) = \frac{\exp(\theta^T_k z_i)}{\sum_{j'} \exp(\theta_{j_i}^T z_i)}\]
である.ただし\(\theta = [\theta_1, ..., \theta_k] \in \mathbf{R}^{d_z \times K}, f_\theta: Z \rightarrow Y \subset \mathbf{R}^K\) .

\(f_\theta\)と\(\phi_W\)によってこのモデルの分布\(Q_{\theta, W}\)が決まる.auxiliary distribution Pを用意すると,KL divergenceは
\[D_{KL}(Q||P) = E_Q [\log Q(X)/P(X)] = \frac{1}{N} \sum_I^N \sum_j^K p_{ij} \log \frac{p_{ij}}{q_{ij}}\]
また,殆どのデータ点を一つのクラスターに入れてしまうような解を避けるため,regularization項を追加する.そのため,Pのラベルの頻度分布\(f_j = \frac{1}{N} \sum_i p_{ij}\)と,事前知識から得られるラベルの一様分布\(\mathbf{u}\)(ここでは一様分布)を定義して,
\[ \begin{aligned}L &= D_{KL}(P||Q) + D_{KL} (\mathbf{f} || \mathbf{u}) \\&=\frac{1}{N} \sum_{i}^N \sum_j^K \left[q_{ij} \log \frac{q_{ij}}{p_{ij}} + q_{ij} \log \frac{f_j}{u_j}\right] \end{aligned}\]
と目的関数を定める.\(L\)を最小化する\(P\)は
\[p_{ij} = \frac{q_{ij} / (\sum_{i'} q_{i'j})^{1/2}}{\sum_{j'} q_{ij'} / (\sum_{i'} q_{i'j'})^{1/2}}\]
さらに\(Q\)を更新するための目的関数は通常のクロスエントロピーと同じ
\[-\frac{1}{N} \sum_i \sum_j p_{ij} \log q_{ij}\]
で,backpropagationによってNNのパラメーターを更新できる.

DEPICT

decoderとパラメータを共有する2つのAEを用意し,片方(corrupted pathway)にはノイズをかけた画像,もう一方(clean pathway)にはクリーンな入力を与える. パラメータの更新はもっぱらclean pathwayで行う(更新の結果はcorrupted pathwayにも適用される). corrupted pathwayが\(Q\)を計算することでより頑強な分布\(Q\)を得られ,clean pathwayが\(P\)を計算し,パラメータ更新をすることでより精度の高いauxiliary distributionを得られるとしている.
NNの目的関数は\(l=0, ..L-1\)をAEの\(l\)層として
\[\frac{1}{N} \sum_i \sum_j p_{ij} \log \tilde{q_{ij}} + \frac{1}{N} \sum_i \sum_{l=0}^{L-1} \frac{1}{|z^l_i|} \|z^l_i - \hat{z}^l_i\|^2\]
とし,backpropagationによってパラメータを更新する.

IV 性能比較

accuracy/normalized mutual information	MNIST-FULL	USPS
DEC	0.844/0.816	0.702/0.693
DCEC	0.890/0.885	0.790/0.826
DEPICT	0.965/0.917	0.964/0.927

DCECはその論文から,DECとDEPICTはDEPICT