MIT OCW, Machine Learning 15日目

Rohit Singh, Tommi Jaakkola, and Ali Mohammad. 6.867 Machine Learning. Fall 2006. Massachusetts Institute of Technology: MIT OpenCourseWare, https://ocw.mit.edu. License: Creative Commons BY-NC-SA.
Lecture 19, 20.

• • Markov chains(cont’d)
    • State prediction
    • Estimation
  • Hidden Markov Models
    • Probability model
  • Three problems to solve
    • Problem 1.
    • Problem 2. most likely hidden state sequence (Viterbi)
      • Example
    • Problem 3: estimation
      • Multiple (partial) alignment

$q$は初期分布，$k$はstateの数とする.またMarkov chainの初期のstateは$X_1$である.

Markov chains(cont’d)

Markov chainを記述する方法には2つある． state transition diagramとgraphical modelである. transition diagramはstateたちをノードとし，遷移確率が0でないstateをつないだ有向グラフであって,例えばfig.1のようである． また，初期分布を,特別に設定したnull stateからの遷移とみてグラフに書き込むことも出来る.
graphical modelでは対照的に，確率変数たちの独立/従属関係に着目する. ある時刻におけるstate $X_t$は確率変数であって，$X_{t-1}$と独立でないことがMarkov chainの定義から言える. ある頂点(state)がほかのある頂点(state)に従属しているときに有向辺によってその従属関係を示して，graphical modelを構成する．つまり,
$X_{t-1} \rightarrow X_t \Leftrightarrow$ $X_t$は$_{t-1}$に従属する
という規則をグラフ化する. fig.2 がその例である.

State prediction

$$P(X_{t+m} = j|X_t = i) = [P^m]_{ij}$$
から，任意の$n$に
$$P(X_n = j) = \sum_{i=1}^k q(i) P(X_n = j| X_1 = i) = \sum_{i=1}^k q(i) [P^{n-1}]_{ij}$$
が成立する. $q^T P^{n-1}$は$j$番目の要素が$P(X_n=j)$であるような横ベクトルであって，
$$\alpha_t^T = q^T \underline{PP\cdots PP}_{t-1 \text{ times}}$$
と書くことにすると,
$$\begin{aligned} q^T &= \alpha_1^T \\ \alpha^T_{t-1}P &= \alpha_t^T, t>1 \\ \sum_{i=1}^k \alpha_{t-1}(i) P_{ij} &=\alpha_t (j) \end{aligned}$$
が成立する.

Estimation

sample pathの観測からMakov chainのtransition matrixを推測することが出来る.
$\{X_t\}$の現れ(sample path)の$x_1,....,x_n$が与えられたとき，そのlog-likelihoodは,
$\hat{n}(i,j)$を$x_1,...,x_n$においてみられた$i$から$j$への推移の回数とすると,
$$\begin{aligned} \log P(x_1,..,x_n) &= \log \left[ P(X_1 = x_1) \prod_{t=1}^{n-1}P(X_{t+1}=x_{t+1}|X_t=x_t) \right] \\ &= \log q(x_1)+\sum_{t=1}^{n-1} \log P_{x_t, x_{t+1}} \\ &= \log q(x_1) + \sum_{i,j} \hat{n}(i,j)\log P_{ij} \end{aligned}$$
であって，$\sum_j P_{ij} = 1$を考えれば，transition matrix $P$の最尤推定は
$$\hat{P}_{ij} = \frac{\hat{n}(i,j)}{\sum_{j'} \hat{n}(i, j')}$$
である. しかし，初期分布$q$を推測するには多くのsample path が必要不可欠である.

Hidden Markov Models

Hidden Markov Models (HMMs)は,観測している値が，直接観測されないMarkov chainが更に確率的に生成しているものであると仮定したモデルである. HMMモデルは広く利用され，例えば，あとで発話をphoneme(音素)のMarkov chainでHMM化し，また，アミノ基の列であるタンパク質をモデル化するのに，タンパク質分子をその構造的特徴のMarkov chainによってHMM化する．
HMMはMarkov chainとmixture modelによって理解できる. fig.3の単純な例を議論する. 時刻は$t=1,2,3,4$の４つだけで，fig.3.aは何度かの観測によって得られた値$y_1,..,y_4$の複数のプロットである． 一旦時刻の情報を捨て去って，$y$の値だけを基準にクラスタリングすると，two component mixture
$$P(y) = \sum_{j=1}^2 P(j) P(y|j)$$
でうまくモデル化出来る. 例えば$P(y|j)\sim N(y; \mu_j, \sigma_j^2)$などとできる. このmixture modelから(まだ時刻を無視しつつ)各時刻でsampleを生成すると，fig.3.bの楕円の中に収まるようになる． このとき，各時刻における観測値のサンプル$y_t$は,選ばれたコンポーネント$x_t$からのみ生成される(fig.4).
各時刻で正しい方の楕円でのみsampleを生成させるためにMarkov chainを使う． Markov chainによって正しい方のcomponentを選ぶようにするのである. すなわち，$t=2$でのcomponentを,$t=1$で選んだcomponentによって選ぶ(fig.5).

Probability model

HMMをgraphical modelで書くことによって，全ての確率変数に対する同時確率を簡単に書き下せる. グラフはどの変数がどの変数に依存しているかを明確にし，どの条件付き確率が同時確率のfactorであるかがわかる． fig.5では，
$$\begin{aligned} P(x_1,...,x_n,y_1,..,y_n) &= P(x_1)P(y_1|x_1)P(x_2|x_1)P(y_2|x_2)\cdots \\&=P(x_1)P(y_1|x_1)\prod_{t=1}^{n-1}[P(x_{t+1}|{x_t)P(y_{t+1}|x_{t+1})]} \\ &= q(x_1)P(y_1|x_1) \prod_{t=1}^{n-1} [P_{x_t, x_{t+1}} P(y_{t+1}|x_{t+1})]\end{aligned}$$
である.

Three problems to solve

1. 観測値の確率を評価する
   $$P(y_1,...,y_n) = \sum_{x_1,...,x_n} P(x_1,...,x_n,y_1,..,y_n)$$
2. 観測値$\{y_i\}$が与えられたとき，最もありそうな隠れたMarkov path $\{x_i^*\}$を推測する.
   $$\{x_1^*, ..., x_n^*\} = \arg \max_{x_1,...,x_n} P(x_1,..,x_n,y_1,..,y_n)$$
3. 時系列に沿った観測値の集合の集合 $\{\{y^{(l)}_i\}_{i=1}^{n_l}\}_{l=1}^L$から,モデルのパラメータを推測する．

Problem 1.

$\alpha_t(j) = P(y_1,...,y_t, X_t=j) ,\beta_t(i) = P(y_{t+1},...,t_n|X_t=i)$として，
$\alpha_t$を$t=1,2,...$と計算していくアルゴリズム(forward algorithm)と,$\beta_t$を$t=n, n-1, ...$と計算していくアルゴリズム(backward algorithm)があり，どちらか一方だけでも計算できるのだが，計算ステップ($t$)が多くなるほど計算量が幾何級数的に増大するので，前後から挟み撃ちして効率的に計算する．
以下はforward algorithmの導出だが，backwardの場合も殆ど同様である.

$$D_y = diag(P(y|1), ..., P(y|k))$$
によって
$$q^T D_{y_1} \mathbf{1} = \sum_{i=1}^k q(i) P(y_1|i)=P(y_1)$$
などと計算できる. 同様に
$$q^T D_{y_1} P D_{y_2} \mathbf{1} = \sum_{i=1}^k \left[q(i)P(y_1|i) \sum_{j=1}^k P_{ij} P(y_2|j)\right] = P(y_1,y_2)$$
これを繰り返して，
$$q^TD_{y_1}PD_{y_2}P \cdots PD_{y_n} \mathbf{1} = P(y_1,...,y_n)$$
が得られる. $\alpha_t(j) = P(y_1,...,y_t, X_t=j)$とすると,
$$\begin{aligned} q^T D_{y_1} &= \alpha_1^T \\ \alpha^T_{t-1}PD_{y_t} &= \alpha^T_t \text{ or equivalently} \\ \left(\sum_{i=1}^k \alpha_{t-1}(i) P_{ij} \right)P(y_t|j) &=\alpha_t(j) \end{aligned}$$

さらに$\beta_t(i) = P(y_{t+1},...,t_n|X_t=i)$とすると，
$$\begin{aligned} \beta_n &= \mathbf{1} \\ \beta_t &= PD_{y+1} \beta_{t+1} \text{ or equivalently} \\ \beta_t(i) &= \sum_{j=1}^k P_{ij}P(y_{t+1}|j)\beta_{t+1}(j) \end{aligned}$$
である.組み合わせて
$$P(y_1,..,y_n) = \alpha^T_t \beta_t = \sum_{i=1}^k \alpha_t(i)\beta_t(i)$$
が任意の$t$に成立する.
これは，
$$P(y_1,..,y_n) = \underline{q^T D_{y_1} P \cdots PD_{y_t}}_{\alpha_t^T} \underline{PD_{y_t+1}\cdots PD_{y_n} \mathbf{1}}_{\beta_t}$$
と理解でき，あるいはMarkov propertyによって
$$\begin{aligned}P(y_1,...,y_n) &= \sum_{i=1}^k \underline{P(y_1,...,y_t, X_t=i)}_{\alpha_t(i)} \underline{P(y_{t+1},...,y_n|X_t=i)}_{\beta_t(i)} \\ & = \sum_{i=1}^k P(y_1,...,y_t,X_t=i) = \sum_{i=1}^k \alpha_n(i) =P(y_1,..,y_n) \end{aligned}$$
からも理解できる.

Problem 2. most likely hidden state sequence (Viterbi)

目的は
$$\max_{x_1,...,x_n} P(y_1,..,y_n,x_1,...,x_n) = P(y_1,...,y_n,x_1^*,...,x_n^*)$$
なる$\{x_t^*\}$を求めることだった.
$$d_t(j) = \max_{x_1,...,x_{t-1}} P(y_1,...,y_t,x_1,..,x_{t-1},X_t=j)$$
とすると，
$$\begin{aligned} q(j) P(y_1|j) &= d_1(j) \\ (\max_i d_{t-1}(i)P_{ij})P(y_t|j) &= d_t(j) \end{aligned}$$
が計算できる. $\max_{x_1,...,x_n}P(y_1,....,y_n,x_1,...,x_n) = \max_j d_n(j)$であって，これによって
$$x_n^* = \arg \max_j d_n(j)$$
が得られて，これを起点として
$$x^*_t = \arg \max_i d_t(i) P_{i, x^*_{t+1}}$$
によって，$x^*_{n-1}, x^*_{n-2},...,x^*_1$を計算していく.
このように，forwad algorithmによって$d_t(j)=\max_{x_1,...,x_{t-1}}P(y_1,...,x_{t-1},X_t=j)$の最大値を$j\in \{1,...,k\}$ごとに計算し,さらにbackward algorithmによって,具体的に$P(y_1,..,x_n)$を最大化する$x_n^*,...,x_1^*$を求めていくアルゴリズムをViterbi Algorithmという.

Example

fig.1で表されるHMMを例に上のアルゴリズムを考察する．state $j=1,2$が選ばれると，，$P(y|j) = N(y, \mu_j, \sigma^2)$によって観測される値が確率的に決まるとし，$\mu_1=3, \mu_2=1$,$\sigma^2$は$j=1,2$で共通とする．観測点は$y_1,...,y_8$が与えられていて，$x_1^*,...,x_8^*$を推測する.
まず，$y_1,...,y_8$が,$\sigma^2$の変化によってどう振る舞うかを見る． $\sigma^2$が大きいとき，$P(y|1),P(y|2)$はほとんど同じ分布になり,観測値が役に立たなくなる．
$d_1(1)/d_1(2)=1, d_2(1)/d_2(2)=1/2, d_3(1)/d_3(2)=1/4,...$と近似できるから,$x_i^*=2$となる．
$\sigma^2$が非常に小さい時，今度はほとんど観測値と制約条件だけが推測に影響するようになる．というのは，
$$\frac{d_t(1)}{d_t(2)}=\underline{\frac{\max_i d_{t-1}(i)P_{i1}}{\max_i d_{t-1}(i)P_{i2} }}_{(1)}\cdot\underline{ \frac{P(y_t|j)}{P(y_t|2)}}_{(2)}$$
において，(2)の部分が極めて大きな，あるいは極めて小さな値を取るようになり，(1)の部分をほとんど無視できるからである.
$\sigma^2$が極端な値でない場合には,Markov chainのtransition matrixからstate 2へできるだけ早く移ろうとする性質と，観測値に合ったhidden pathを辿ろうとする性質のバランスを取ろうとする． 例えば$\sigma^2=1$なら，most likely state sequenceは1122222である．

Problem 3: estimation

Hidden statesを観測できず，そこから確率的に生成される値のみを観測できるというのは，モデルの全ての変数を知ることなくモデルを推測しようとしているという点でmixture modelと似ている． この問題はmixture modelと同様にEM algorithmを反復的に用いることで解ける． 普通は複数回行われる，すなわち$\{\{y_t\}_1^n\}_{p=1}^q$のように観測値が得られるのだが，簡単のために$q=1$すなわち観測値は１通りしか無いとする．
EM-algorithmを導く簡単な方法は，まずは全ての変数が観測されているとしてモデルを構成することである．
$$\begin{aligned} \delta(i|t) &= \begin{cases} 1 \ \ \ &(x_t=i) \\ 0 &otherwise \end{cases} \\ \delta(i,j|t) &= \begin{cases} 1 \ \ \ &(x_t=i, x_{t+1}=j) \\ 0 & otherwise \end{cases} \end{aligned}$$
とすると，complete log-likelihoodは
$$\begin{aligned} l(\{x_t\},\{y_t\}) = & \underline{\sum_{i=1}^k \delta(i|1)\log q(i)}_{(1)} + \underline{\sum_{i=1}^k \left(\sum_{t=1}^n \delta(i|t) \log P(y_t|i) \right)}_{(2)} \\ &+ \underline{\sum_{i=1}^k \sum_{j=1}^k \left(\underline{\sum_{t=1}^n \delta(i,j|t)}_{(3)}\right) \log P_{ij}}_{(4)}\end{aligned}$$
(1): 初期状態の確率
(2): 各state $i$における，$y$を生成する確率を$i \in \{1,...,k\}$での総和
(3): $x_1,...,x_n$で$i\rightarrow j$の遷移が起きる回数
(4): 全てのstateの組で，遷移がどれほど起こるかの総和

$\delta$を緩和させた”soft”なカウント$p$を
$$\begin{aligned} p(i|t) &= P(X_t = i|y_1,...,y_n) \\ p(i,j|t) &= P(x_t=i,X_{t+1}=j|y_1,...,y_n) \end{aligned}$$
と定める.
$$P(y_1,..,y_n,X_t=i) = P(y_1,...,y_t,X_t=i)P(y_{t+1},..,y_n|X_t=i)=\alpha_t(i)\beta_t(i)$$
だから，posteriorは
$$P(X_t=i|y_1,...,y_n) = \frac{\alpha_t(i)\beta_t(i)}{\sum_{i'=1}^k \alpha_t(i')\beta_t(i')}$$
という正規化で計算できて，同様に
$$\begin{aligned} P&(y_1,...,y_n,X_t=i,X_{t+1}=j) \\ &=P(y_1,...,y_t,X_t=i)P_{ij}P(y_{t+1}|j)P(y_{t+2},...,y_n|X_{t+1}=j) \\ &= \alpha_t(i) P_{ij} P(y_{t+1}|j)\beta_{t+1}(j) \end{aligned}$$

したがって
$$P(X_t=i, X_{t+1}=j|y_1,....,y_n) = \frac{\alpha_t(i)P_{ij}P(y_{t+1}|j)\beta_{t+1}(j)}{\sum_{i'=1}^k \sum_{j'=1}^k \alpha_t(i')P_{i'j'}P(y_{t+1}|j')\beta_{t+1}(j')}$$

Multiple (partial) alignment

複数の列が与えられるとき，その類似点をさがすのがalignment問題である. そのパターンは，全ての列に存在するということの他にはほとんど情報が得られていないとする． 簡単のため，そのパターンは長さ4であることは既知とする． この状況で考えられる最も簡単なHMMはfig.2である．$m_1,..,m_4$というstatesは”match states”といって，求めるべきパターンを生成したであろうstatesである． $I_1, I_2$は”insert states”であって，探しているパターン以外の列を生成する. それぞれのstateは$P(y|I_i), i=1,2, P(y|m_i) , i=1,...4$というoutput distributionをもつ.これらの分布と$p$の値を与えられた列たちから推測する.

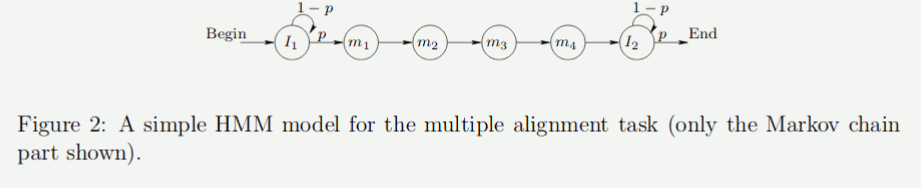
このモデルは有限長の列を生成する. $I_1$に入って最初の要素を生成し，平均$1/p$ステップ$I_1$にとどまった後,$m_1$に遷移してパターンを生成し，$I_2$に遷移してまた平均$1/p$ステップとどまってから列を終わらせる.
複数の列が与えられたとき，このHMMのパラメータを,EM algorithmによって最尤推定する. ここではまだどこが生成されたパターンなのかは考えず，単にパラメータを最適化する. パラメータが見つかったら，Viterbi algorithmによってそれぞれの観測点がどのhidden stateによって生成されたかを推測する.例えば観測列$y_1,...,y_n$に
$$\begin{array}{} \text{hidden} &I_1 & I_1 & \cdots & I_1 & m_1 & m_2 & m_3 & m_4 & I_2 & I_2 & \cdots & I_2 \\ \text{observation} &y_1 & y_2 & \cdots & y_{t-1} & y_t & y_{t+1} & y_{t+2} & y_{t+3} & y_{t+4} & y_{t+5} & \cdots & y_n\end{array}$$
という対応の推測が得られたとき,hiddenの列とobesrvationの列には一対一の関係が有り，この例では，パターンは$t$において，すなわちmatch statesが始まったところで始まる．
それぞれの観測列でのパターンの部分列はfig.3のようにアラインされる．

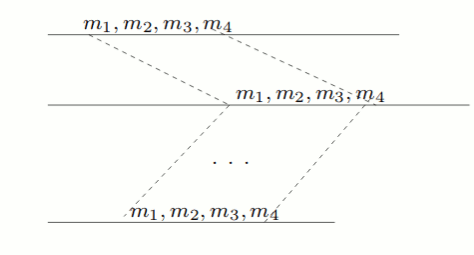
figure 3