MIT OCW, Machine Learning 16日目

Rohit Singh, Tommi Jaakkola, and Ali Mohammad. 6.867 Machine Learning. Fall 2006. Massachusetts Institute of Technology: MIT OpenCourseWare, https://ocw.mit.edu. License: Creative Commons BY-NC-SA.

• • Bayesian networks
    • Marginal independence and induced dependence
      • Explaining away
      • Bayesian networks and conditional independence
      • Graph and the probability distribution

Bayesian networks

Bayesian networkは確率的な情報を表現し,使うのに有用なモデルである. Bayesian networkは1. 有向グラフと,2. それに付随する確率分布からなる. グラフは確率変数たちの質的な関係(条件付き独立性)を表現し,確率分布は確率変数たちの量的な関係を記述する. HMMでforward-backward algorithmが効率的であったのはMarkov性ゆえであり,これをBayesian networkの場合にも一般化するため,確率変数同士の独立性,条件付き独立性,従属性を明確に記述するグラフは非常に重要である.
まずは単純なBayesian networkを挙げる(fig.1). 確率変数$x_1, x_2$は独立なコイントスの結果で,$0, 1$のどちらかの値を取る. また$x_3=\delta(x_1,x_2), \text{ Kronecker's delta}$で確率変数$x_3$を定義する. 状況設定から同時分布は
$$P(x_1, x_2, x_3) = P(x_1)P(x_2)P(x_3|x_1,x_2)\ \ \ \ (1)$$
とわかるが,同じ分布をfig.1のグラフだけから導ける. その前にいくつかの用語を定義する.
$x_1$から$x_3$への辺が有るから,$x_1$は$x_3$のparent(親)であり,$x_3$は$x_1$のchild(子)であるという. $x_2$もまた$x_3$の親であり,このとき$x_3$は$x_1$と$x_2$に従属する. グラフに合致した同時確率分布は必ず,それぞれの確率変数の親たちによって条件付けられた条件付き確立の積として書ける. よって(1)はfig.1のグラフと合致している.

Marginal independence and induced dependence

$$\begin{aligned} P(x_1, x_2) &= \sum_{x_3}P(x_1,x_2,x_3)=\sum_{x_3}P(x_1)P(x_2)P(x_3|x_1,x_2)\\ &=P(x_1)P(x_2)\sum_{x_3}P(x_3|x_1,x_2)=P(x_1)P(x_2) \end{aligned}$$
このように,他の確率変数を無視すると周辺分布が独立になるとき,marginary independentであるという. これはグラフからも見て取れる.

確率変数のもう一つの典型的な関係はinduced dependenceである. $x_1, x_2$の現れを与えられず,$x_3$の現れのみを与えられた場合を考える.$x_3=1$ならば$x_1=x_2=1$か$x_1=x_2=0$のどちらかに決まり,$x_3=0$ならば$x_2 = 1-x_1$に決まるから,$x_1$が決まれば$x_2$が決まるし,$x_2$が決まれば$x_1$が決まる. すなわち$x_3$が決定されると$x_1,x_2$はdependentな関係になる. これは後で述べる方法によってグラフから見て取れる.

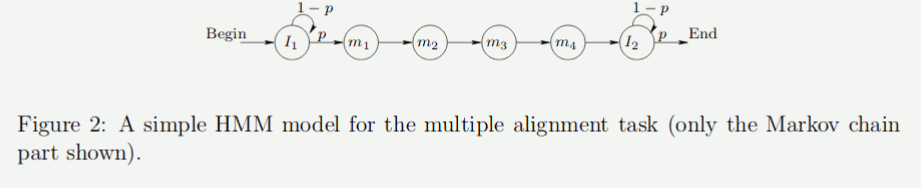
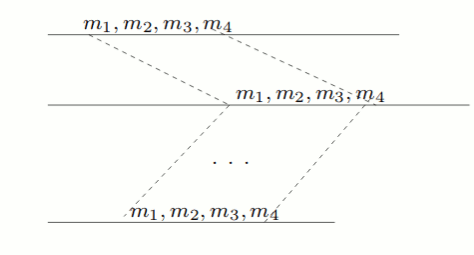
marginal independence とinduced dependenceは現実のモデルでよく現れる.　fig.2cのfactorial Hidden Markov Modelはその例である. このモデルでは2つの周辺独立なMarkov chainが観測値を作り出している. 換言すれば,2つのMarkov chainが観測値によってのみ結び付けられているということである(induced dependence). このモデルからサンプリングするには,2つのMarkov modelから独立にサンプリングを行い,各時点において2つのstateから観測値をサンプリングする. fig.2cの同時分布は
$$P(x_1')P(x_1)P(y_1|x_1',x_1)P(x_2'|x_1')P(x_1|x_1)P(y_2|x_2,x_2')P(x_3'|x_2')P(x_3|x_2)P(y_3|x_3,x_3')$$
とfactorizationできる. このモデルは例えば二人が話しているのを1つのマイクで録音し,それぞれの人が何を話したか推測したり,2つのハプロタイプから生成された表現型からもとのハプロタイプを推測するのに利用できる.

Explaining away

また,Bayesian networkでうまく把握できる確立モデルにexplaning awayがある.Pearl, 1988による,強盗警報機の鳴る原因のモデル(fig.3)を例に見る. 4つの二値(0, 1)確率変数$A, B, E, R$があって,
$A$は警報機,$B$,$E$は地震,$R$はラジオで地震情報がなされていることを代表している.
$P(E=1)=P(B=1) \sim 0,P(A=1|E,B) \sim (E \lor B),P(R=1|E=1)\sim 1, P(R=1|E=0)=0$
を仮定する. fig.3で影のついた確率変数の情報のみを持っているとする.
$A=1$のみが解っているときを考える(fig.3.b).$E=1$か$B=1$の少なくとも一方が成立しているとわかるが,$E,B$ともに滅多に生じない事象だから,$B=E=1$は必ず起きないと仮定する. この仮定のもとで$R=1$の情報を得たら$E=1,B=0$を確信し,$B=1$を排除(explain away)できる. したがって
$$P(E=1|A=1,R=1) \sim 1, \ \ P(B=1|A=1,R=1)\sim 0$$
である. ここで$R,B$は$A=1$のもとで条件付き従属であることを使った.これもまたグラフから見て取れる性質である.

Bayesian networks and conditional independence

グラフはもともと変数の独立性をencodeしているから,その独立性をextractするための基準が必要である. Bayesian networkの場合,この基準をD-separtation criterionという.

例えば先程のモデルを拡張したfig.4aを考える.ここで$L$は,警報がなったので帰宅したという事象を代表する変数である. $R,B$は$A$のもとで独立か否かと言った問いに答えるための手順を考える.
1. 対象の変数のancestral graphを構成する. ここでは対象とは$R,B,A$であって,ancestral graphはこれらとともに,これらの変数に至る有向辺を何ステップでも辿って現れる変数全てを含む. 今の場合,ancestral graphはfig.4bである.
2. 得られたancestral graphにおいて,子ノードを共有するノード間に無向辺を加える. 3つ以上のノードが子ノードを共有する場合には,それらのつくる全てのペアについて辺を加える(fig.4c).これをmoralizeという.
3. 全ての有向辺を無向辺に置き換え,無向グラフ(fig.4d)を得る.

結果得られた無向グラフから,もとの問の答えを読み取れる. 得られた無向グラフから$A$とそれに結ばれた辺を取り去ったとき,$R$と$B$を結ぶpathが存在しなければ$R,B$は$A$によって条件付き独立であり,存在すれば条件付き独立であると言える. したがってfig.4dから,$R,B$は$A$によって条件付き従属である.

fig.1に立ち返り,D-separated criterionを使うと,fig.5によって$x_1,x_2$がmarginally independentであることが見て取れるし,fig.6から$x_1,x_2$が$x_3$によって条件付従属であることが見て取れる.

Graph and the probability distribution

以上の議論は,グラフとそれに対応付けられる確率分布がconsistentであるときにのみ成立する. consistentとは,グラフから見て取れる全ての(条件付き含む)独立性が,確率分布の上でも言えるということである. グラフから見て取れる独立性というのは数多く存在する.
$d$個のノードをもつ循環しないグラフ$G$が与えられたとき,
$$P(x_1,...,x_d)=\prod_{i=1}^d P(x_i| x_{{pa}_i})$$
はそのグラフとconsistentであることが知られている.ただし$pa_i$は$x_i$の親ノードの集合である.

MIT OCW, Machine Learning 15日目

Rohit Singh, Tommi Jaakkola, and Ali Mohammad. 6.867 Machine Learning. Fall 2006. Massachusetts Institute of Technology: MIT OpenCourseWare, https://ocw.mit.edu. License: Creative Commons BY-NC-SA.
Lecture 19, 20.

• • Markov chains(cont’d)
    • State prediction
    • Estimation
  • Hidden Markov Models
    • Probability model
  • Three problems to solve
    • Problem 1.
    • Problem 2. most likely hidden state sequence (Viterbi)
      • Example
    • Problem 3: estimation
      • Multiple (partial) alignment

$q$は初期分布，$k$はstateの数とする.またMarkov chainの初期のstateは$X_1$である.

Markov chains(cont’d)

Markov chainを記述する方法には2つある． state transition diagramとgraphical modelである. transition diagramはstateたちをノードとし，遷移確率が0でないstateをつないだ有向グラフであって,例えばfig.1のようである． また，初期分布を,特別に設定したnull stateからの遷移とみてグラフに書き込むことも出来る.
graphical modelでは対照的に，確率変数たちの独立/従属関係に着目する. ある時刻におけるstate $X_t$は確率変数であって，$X_{t-1}$と独立でないことがMarkov chainの定義から言える. ある頂点(state)がほかのある頂点(state)に従属しているときに有向辺によってその従属関係を示して，graphical modelを構成する．つまり,
$X_{t-1} \rightarrow X_t \Leftrightarrow$ $X_t$は$_{t-1}$に従属する
という規則をグラフ化する. fig.2 がその例である.

State prediction

$$P(X_{t+m} = j|X_t = i) = [P^m]_{ij}$$
から，任意の$n$に
$$P(X_n = j) = \sum_{i=1}^k q(i) P(X_n = j| X_1 = i) = \sum_{i=1}^k q(i) [P^{n-1}]_{ij}$$
が成立する. $q^T P^{n-1}$は$j$番目の要素が$P(X_n=j)$であるような横ベクトルであって，
$$\alpha_t^T = q^T \underline{PP\cdots PP}_{t-1 \text{ times}}$$
と書くことにすると,
$$\begin{aligned} q^T &= \alpha_1^T \\ \alpha^T_{t-1}P &= \alpha_t^T, t>1 \\ \sum_{i=1}^k \alpha_{t-1}(i) P_{ij} &=\alpha_t (j) \end{aligned}$$
が成立する.

Estimation

sample pathの観測からMakov chainのtransition matrixを推測することが出来る.
$\{X_t\}$の現れ(sample path)の$x_1,....,x_n$が与えられたとき，そのlog-likelihoodは,
$\hat{n}(i,j)$を$x_1,...,x_n$においてみられた$i$から$j$への推移の回数とすると,
$$\begin{aligned} \log P(x_1,..,x_n) &= \log \left[ P(X_1 = x_1) \prod_{t=1}^{n-1}P(X_{t+1}=x_{t+1}|X_t=x_t) \right] \\ &= \log q(x_1)+\sum_{t=1}^{n-1} \log P_{x_t, x_{t+1}} \\ &= \log q(x_1) + \sum_{i,j} \hat{n}(i,j)\log P_{ij} \end{aligned}$$
であって，$\sum_j P_{ij} = 1$を考えれば，transition matrix $P$の最尤推定は
$$\hat{P}_{ij} = \frac{\hat{n}(i,j)}{\sum_{j'} \hat{n}(i, j')}$$
である. しかし，初期分布$q$を推測するには多くのsample path が必要不可欠である.

Hidden Markov Models

Hidden Markov Models (HMMs)は,観測している値が，直接観測されないMarkov chainが更に確率的に生成しているものであると仮定したモデルである. HMMモデルは広く利用され，例えば，あとで発話をphoneme(音素)のMarkov chainでHMM化し，また，アミノ基の列であるタンパク質をモデル化するのに，タンパク質分子をその構造的特徴のMarkov chainによってHMM化する．
HMMはMarkov chainとmixture modelによって理解できる. fig.3の単純な例を議論する. 時刻は$t=1,2,3,4$の４つだけで，fig.3.aは何度かの観測によって得られた値$y_1,..,y_4$の複数のプロットである． 一旦時刻の情報を捨て去って，$y$の値だけを基準にクラスタリングすると，two component mixture
$$P(y) = \sum_{j=1}^2 P(j) P(y|j)$$
でうまくモデル化出来る. 例えば$P(y|j)\sim N(y; \mu_j, \sigma_j^2)$などとできる. このmixture modelから(まだ時刻を無視しつつ)各時刻でsampleを生成すると，fig.3.bの楕円の中に収まるようになる． このとき，各時刻における観測値のサンプル$y_t$は,選ばれたコンポーネント$x_t$からのみ生成される(fig.4).
各時刻で正しい方の楕円でのみsampleを生成させるためにMarkov chainを使う． Markov chainによって正しい方のcomponentを選ぶようにするのである. すなわち，$t=2$でのcomponentを,$t=1$で選んだcomponentによって選ぶ(fig.5).

Probability model

HMMをgraphical modelで書くことによって，全ての確率変数に対する同時確率を簡単に書き下せる. グラフはどの変数がどの変数に依存しているかを明確にし，どの条件付き確率が同時確率のfactorであるかがわかる． fig.5では，
$$\begin{aligned} P(x_1,...,x_n,y_1,..,y_n) &= P(x_1)P(y_1|x_1)P(x_2|x_1)P(y_2|x_2)\cdots \\&=P(x_1)P(y_1|x_1)\prod_{t=1}^{n-1}[P(x_{t+1}|{x_t)P(y_{t+1}|x_{t+1})]} \\ &= q(x_1)P(y_1|x_1) \prod_{t=1}^{n-1} [P_{x_t, x_{t+1}} P(y_{t+1}|x_{t+1})]\end{aligned}$$
である.

Three problems to solve

1. 観測値の確率を評価する
   $$P(y_1,...,y_n) = \sum_{x_1,...,x_n} P(x_1,...,x_n,y_1,..,y_n)$$
2. 観測値$\{y_i\}$が与えられたとき，最もありそうな隠れたMarkov path $\{x_i^*\}$を推測する.
   $$\{x_1^*, ..., x_n^*\} = \arg \max_{x_1,...,x_n} P(x_1,..,x_n,y_1,..,y_n)$$
3. 時系列に沿った観測値の集合の集合 $\{\{y^{(l)}_i\}_{i=1}^{n_l}\}_{l=1}^L$から,モデルのパラメータを推測する．

Problem 1.

$\alpha_t(j) = P(y_1,...,y_t, X_t=j) ,\beta_t(i) = P(y_{t+1},...,t_n|X_t=i)$として，
$\alpha_t$を$t=1,2,...$と計算していくアルゴリズム(forward algorithm)と,$\beta_t$を$t=n, n-1, ...$と計算していくアルゴリズム(backward algorithm)があり，どちらか一方だけでも計算できるのだが，計算ステップ($t$)が多くなるほど計算量が幾何級数的に増大するので，前後から挟み撃ちして効率的に計算する．
以下はforward algorithmの導出だが，backwardの場合も殆ど同様である.

$$D_y = diag(P(y|1), ..., P(y|k))$$
によって
$$q^T D_{y_1} \mathbf{1} = \sum_{i=1}^k q(i) P(y_1|i)=P(y_1)$$
などと計算できる. 同様に
$$q^T D_{y_1} P D_{y_2} \mathbf{1} = \sum_{i=1}^k \left[q(i)P(y_1|i) \sum_{j=1}^k P_{ij} P(y_2|j)\right] = P(y_1,y_2)$$
これを繰り返して，
$$q^TD_{y_1}PD_{y_2}P \cdots PD_{y_n} \mathbf{1} = P(y_1,...,y_n)$$
が得られる. $\alpha_t(j) = P(y_1,...,y_t, X_t=j)$とすると,
$$\begin{aligned} q^T D_{y_1} &= \alpha_1^T \\ \alpha^T_{t-1}PD_{y_t} &= \alpha^T_t \text{ or equivalently} \\ \left(\sum_{i=1}^k \alpha_{t-1}(i) P_{ij} \right)P(y_t|j) &=\alpha_t(j) \end{aligned}$$

さらに$\beta_t(i) = P(y_{t+1},...,t_n|X_t=i)$とすると，
$$\begin{aligned} \beta_n &= \mathbf{1} \\ \beta_t &= PD_{y+1} \beta_{t+1} \text{ or equivalently} \\ \beta_t(i) &= \sum_{j=1}^k P_{ij}P(y_{t+1}|j)\beta_{t+1}(j) \end{aligned}$$
である.組み合わせて
$$P(y_1,..,y_n) = \alpha^T_t \beta_t = \sum_{i=1}^k \alpha_t(i)\beta_t(i)$$
が任意の$t$に成立する.
これは，
$$P(y_1,..,y_n) = \underline{q^T D_{y_1} P \cdots PD_{y_t}}_{\alpha_t^T} \underline{PD_{y_t+1}\cdots PD_{y_n} \mathbf{1}}_{\beta_t}$$
と理解でき，あるいはMarkov propertyによって
$$\begin{aligned}P(y_1,...,y_n) &= \sum_{i=1}^k \underline{P(y_1,...,y_t, X_t=i)}_{\alpha_t(i)} \underline{P(y_{t+1},...,y_n|X_t=i)}_{\beta_t(i)} \\ & = \sum_{i=1}^k P(y_1,...,y_t,X_t=i) = \sum_{i=1}^k \alpha_n(i) =P(y_1,..,y_n) \end{aligned}$$
からも理解できる.

Problem 2. most likely hidden state sequence (Viterbi)

目的は
$$\max_{x_1,...,x_n} P(y_1,..,y_n,x_1,...,x_n) = P(y_1,...,y_n,x_1^*,...,x_n^*)$$
なる$\{x_t^*\}$を求めることだった.
$$d_t(j) = \max_{x_1,...,x_{t-1}} P(y_1,...,y_t,x_1,..,x_{t-1},X_t=j)$$
とすると，
$$\begin{aligned} q(j) P(y_1|j) &= d_1(j) \\ (\max_i d_{t-1}(i)P_{ij})P(y_t|j) &= d_t(j) \end{aligned}$$
が計算できる. $\max_{x_1,...,x_n}P(y_1,....,y_n,x_1,...,x_n) = \max_j d_n(j)$であって，これによって
$$x_n^* = \arg \max_j d_n(j)$$
が得られて，これを起点として
$$x^*_t = \arg \max_i d_t(i) P_{i, x^*_{t+1}}$$
によって，$x^*_{n-1}, x^*_{n-2},...,x^*_1$を計算していく.
このように，forwad algorithmによって$d_t(j)=\max_{x_1,...,x_{t-1}}P(y_1,...,x_{t-1},X_t=j)$の最大値を$j\in \{1,...,k\}$ごとに計算し,さらにbackward algorithmによって,具体的に$P(y_1,..,x_n)$を最大化する$x_n^*,...,x_1^*$を求めていくアルゴリズムをViterbi Algorithmという.

Example

fig.1で表されるHMMを例に上のアルゴリズムを考察する．state $j=1,2$が選ばれると，，$P(y|j) = N(y, \mu_j, \sigma^2)$によって観測される値が確率的に決まるとし，$\mu_1=3, \mu_2=1$,$\sigma^2$は$j=1,2$で共通とする．観測点は$y_1,...,y_8$が与えられていて，$x_1^*,...,x_8^*$を推測する.
まず，$y_1,...,y_8$が,$\sigma^2$の変化によってどう振る舞うかを見る． $\sigma^2$が大きいとき，$P(y|1),P(y|2)$はほとんど同じ分布になり,観測値が役に立たなくなる．
$d_1(1)/d_1(2)=1, d_2(1)/d_2(2)=1/2, d_3(1)/d_3(2)=1/4,...$と近似できるから,$x_i^*=2$となる．
$\sigma^2$が非常に小さい時，今度はほとんど観測値と制約条件だけが推測に影響するようになる．というのは，
$$\frac{d_t(1)}{d_t(2)}=\underline{\frac{\max_i d_{t-1}(i)P_{i1}}{\max_i d_{t-1}(i)P_{i2} }}_{(1)}\cdot\underline{ \frac{P(y_t|j)}{P(y_t|2)}}_{(2)}$$
において，(2)の部分が極めて大きな，あるいは極めて小さな値を取るようになり，(1)の部分をほとんど無視できるからである.
$\sigma^2$が極端な値でない場合には,Markov chainのtransition matrixからstate 2へできるだけ早く移ろうとする性質と，観測値に合ったhidden pathを辿ろうとする性質のバランスを取ろうとする． 例えば$\sigma^2=1$なら，most likely state sequenceは1122222である．

Problem 3: estimation

Hidden statesを観測できず，そこから確率的に生成される値のみを観測できるというのは，モデルの全ての変数を知ることなくモデルを推測しようとしているという点でmixture modelと似ている． この問題はmixture modelと同様にEM algorithmを反復的に用いることで解ける． 普通は複数回行われる，すなわち$\{\{y_t\}_1^n\}_{p=1}^q$のように観測値が得られるのだが，簡単のために$q=1$すなわち観測値は１通りしか無いとする．
EM-algorithmを導く簡単な方法は，まずは全ての変数が観測されているとしてモデルを構成することである．
$$\begin{aligned} \delta(i|t) &= \begin{cases} 1 \ \ \ &(x_t=i) \\ 0 &otherwise \end{cases} \\ \delta(i,j|t) &= \begin{cases} 1 \ \ \ &(x_t=i, x_{t+1}=j) \\ 0 & otherwise \end{cases} \end{aligned}$$
とすると，complete log-likelihoodは
$$\begin{aligned} l(\{x_t\},\{y_t\}) = & \underline{\sum_{i=1}^k \delta(i|1)\log q(i)}_{(1)} + \underline{\sum_{i=1}^k \left(\sum_{t=1}^n \delta(i|t) \log P(y_t|i) \right)}_{(2)} \\ &+ \underline{\sum_{i=1}^k \sum_{j=1}^k \left(\underline{\sum_{t=1}^n \delta(i,j|t)}_{(3)}\right) \log P_{ij}}_{(4)}\end{aligned}$$
(1): 初期状態の確率
(2): 各state $i$における，$y$を生成する確率を$i \in \{1,...,k\}$での総和
(3): $x_1,...,x_n$で$i\rightarrow j$の遷移が起きる回数
(4): 全てのstateの組で，遷移がどれほど起こるかの総和

$\delta$を緩和させた”soft”なカウント$p$を
$$\begin{aligned} p(i|t) &= P(X_t = i|y_1,...,y_n) \\ p(i,j|t) &= P(x_t=i,X_{t+1}=j|y_1,...,y_n) \end{aligned}$$
と定める.
$$P(y_1,..,y_n,X_t=i) = P(y_1,...,y_t,X_t=i)P(y_{t+1},..,y_n|X_t=i)=\alpha_t(i)\beta_t(i)$$
だから，posteriorは
$$P(X_t=i|y_1,...,y_n) = \frac{\alpha_t(i)\beta_t(i)}{\sum_{i'=1}^k \alpha_t(i')\beta_t(i')}$$
という正規化で計算できて，同様に
$$\begin{aligned} P&(y_1,...,y_n,X_t=i,X_{t+1}=j) \\ &=P(y_1,...,y_t,X_t=i)P_{ij}P(y_{t+1}|j)P(y_{t+2},...,y_n|X_{t+1}=j) \\ &= \alpha_t(i) P_{ij} P(y_{t+1}|j)\beta_{t+1}(j) \end{aligned}$$

したがって
$$P(X_t=i, X_{t+1}=j|y_1,....,y_n) = \frac{\alpha_t(i)P_{ij}P(y_{t+1}|j)\beta_{t+1}(j)}{\sum_{i'=1}^k \sum_{j'=1}^k \alpha_t(i')P_{i'j'}P(y_{t+1}|j')\beta_{t+1}(j')}$$

Multiple (partial) alignment

複数の列が与えられるとき，その類似点をさがすのがalignment問題である. そのパターンは，全ての列に存在するということの他にはほとんど情報が得られていないとする． 簡単のため，そのパターンは長さ4であることは既知とする． この状況で考えられる最も簡単なHMMはfig.2である．$m_1,..,m_4$というstatesは”match states”といって，求めるべきパターンを生成したであろうstatesである． $I_1, I_2$は”insert states”であって，探しているパターン以外の列を生成する. それぞれのstateは$P(y|I_i), i=1,2, P(y|m_i) , i=1,...4$というoutput distributionをもつ.これらの分布と$p$の値を与えられた列たちから推測する.

このモデルは有限長の列を生成する. $I_1$に入って最初の要素を生成し，平均$1/p$ステップ$I_1$にとどまった後,$m_1$に遷移してパターンを生成し，$I_2$に遷移してまた平均$1/p$ステップとどまってから列を終わらせる.
複数の列が与えられたとき，このHMMのパラメータを,EM algorithmによって最尤推定する. ここではまだどこが生成されたパターンなのかは考えず，単にパラメータを最適化する. パラメータが見つかったら，Viterbi algorithmによってそれぞれの観測点がどのhidden stateによって生成されたかを推測する.例えば観測列$y_1,...,y_n$に
$$\begin{array}{} \text{hidden} &I_1 & I_1 & \cdots & I_1 & m_1 & m_2 & m_3 & m_4 & I_2 & I_2 & \cdots & I_2 \\ \text{observation} &y_1 & y_2 & \cdots & y_{t-1} & y_t & y_{t+1} & y_{t+2} & y_{t+3} & y_{t+4} & y_{t+5} & \cdots & y_n\end{array}$$
という対応の推測が得られたとき,hiddenの列とobesrvationの列には一対一の関係が有り，この例では，パターンは$t$において，すなわちmatch statesが始まったところで始まる．
それぞれの観測列でのパターンの部分列はfig.3のようにアラインされる．

figure 3

MIT OCW, Machine Learning 14日目

Rohit Singh, Tommi Jaakkola, and Ali Mohammad. 6.867 Machine Learning. Fall 2006. Massachusetts Institute of Technology: MIT OpenCourseWare, https://ocw.mit.edu. License: Creative Commons BY-NC-SA.
Lecture 18.

• • Specral clustering
    • Graph construction
    • Graph partitioning and criteria
    • Spectral clustering, the eigenvalue problem
    • Spectral clustering, random walk
      • Definition

Specral clustering

データ点の近さの尺度を導入してそれぞれの点同士を頂点とし，辺をその近さの尺度によって重み付けしたグラフを構成できる. spectral clusteringはその重みづけグラフの分割を，固有値問題と考えるアルゴリズムのクラスである. 大きな正の重みで繋がれているノードたちは同じクラスターに入れられることが多い． グラフ表現を行うことで，そのアルゴリズムがノード間の近さだけを基準にして分類を行っていることを際立たせることができる.

Graph construction

ベクトル空間上で表現できる場合にも，グラフ構造での表現には有利な点が有る．例えばfig.1.aの点は2つの半円上の点に分類できるが，これを少数のGaussianの混合で表現することはできない一方，それぞれの点の最近傍の2点をつなげることで,fig.1.bの，非常によく特徴を捉えたグラフが構成できる. このような重み付けグラフを構成するより一般的な方法を議論する. これには多くの方法が有るが，もっとも典型的なのが，上で見たように,k-nearest neighborを使う方法である. すなわち，すべての点について，$k$個の最近傍の点をつなげる無向グラフを作成し，さらに
$$W_{ij} = \begin{cases} \exp(-\beta \|\mathbf{x_i - x_j}\|) \ \ &\text{if } i, j \text{ are connected} \\ 0 & \text{otherwise} \end{cases}$$
によって重みを計算する. $W_{ij} = W_{ji}$である. 対角成分は全て0とする.
$k, \beta$が選べるパラメータである. $k$は求めたいクラスターたちの次元によって適した値が決まってくる．例えば，クラスターが$d$次元の表面をもつとするなら，$k\geq d$が望ましい. 小さな$k$は疎なグラフを作りやすくし，よく似た点たちのみのクラスターが作られるようになる． これは,遠く離れた点ではユークリッド距離を使うのがナンセンスになるような場合に有利である ．例えば球面にのみ全てのデータ点が存在して，点たちの距離が球面に沿った距離で図られるべきときには，点が遠くなれば遠くなるほど，ユークリッド距離と球面上の距離が乖離してくることが想像できるだろう.
$\beta$も同様の役割を果たす．

Graph partitioning and criteria

$n$個の点を2つに分類する問題を定式化する. より多くの種類に分類するときには再帰的に二値分類を適用する. 対象は，重み付け行列$W$で表現されていて，$W$は非負の対称行列で対角成分は0である． $W$を近さの尺度として，ノードたちを$C^+, C^-$の二つに分類する. $y_i = \begin{cases} 1 \ \ & i \in C^+ \\ -1 & i \in C^-\end{cases}$という変数$y=\{y_i\}$を定義する.
$C^+, C^-$を決めれば分類は一意に定まり，その分類(cut)に対する重み
$$s(C^+,C^-)= \sum_{i \in C^+, j\in C^-} W_{ij} = \frac{1}{4}W_{ij} \sum_{i,j} (y_i-y_j)^2 = J(y)$$
を導入する. $i, j$が異なって分類されると$W_{ij}$分の重みが$s$につく． 全てが同じクラスタに分類されるとき$s=0$だから，どちらのクラスタにも同じくらいの数のノードが入るようにするため，minimum cut criterionを導入する. よく使われるcriterionにnormalized cut(Shi and Malik 2000)がある.
$$\text{Norm-cut}(C^+, C^-) = \frac{s(C^+, C^-)}{s(C^+,C^+)+s(C^+,C^-)}+\frac{s(C^+,C^-)}{s(C^-, C^-)+s(C^+,C^-)}$$
である．ただし$s(C^+, C^+)=\sum_{i \in C^+, C^+} W_{i,j}$とする.
この問題を厳密かつ効率的に解く方法は存在しないため，eigenvalue problemによって近似的に解く.

Spectral clustering, the eigenvalue problem

$y= (y_1,..,y_n)$でそれぞれは$\pm 1$のどちらかを取ったが,$z= (z_1,..,z_n)$で$z_i \in \mathbb{R}$に条件を緩和する．やはり$i \in C^+ \Rightarrow z_i >0, i \in C^- \Rightarrow z_i < 0$とする.このように二値分類問題を緩和し，eigenvalue問題に帰着させる．まずはcutの重みを改めて表現する.
$$\begin{aligned} J(z) &= \frac{1}{4} W_{ij}(z_i-z_j)^2 = \frac{1}{4}\sum_{i,j} (z_i^2-2z_iz_j+z_j^2)=\frac{1}{4}\sum_{i,j}W_{ij}(2z_i^2-2z_iz_j) \\ &= \frac{1}{2}\sum_i \underline{(\sum_j W_{ij})}_{D_{ii}}z^2_i + \frac{1}{2} \sum_{i,j} W_{ij}z_iz_j = \frac{1}{2}z^T (D-W)z \end{aligned}$$

$D_{ii}=\sum_j W_{ij}$という対角行列を使って表現した.
$L=D-W$はgraph Laplacianという名でしられ，半正定値行列である. $L$の最小固有値は必ず$0$であり，対応する固有ベクトルは$z=(1,...,1)$である. normalized cut criterionを考慮すると，最適化問題は
$$minimize \frac{1}{2} z^T (D-W)z \ \ \text{ subject to } z^TDz=1, z^TD1=0$$
となる. Lagrange multiplierを使うと,
$$(D-W)z = \lambda Dz$$
の2番目に小さい固有値を求めることと同じになる(らしい). $\hat{y_i} = sign(z_{2_i})$の符号が有るノードが入るクラスターになる.fig.2はあるspectral cluseringの近似解である.

Spectral clustering, random walk

normalized cut problemを緩和して近似的に解いた．全く異なったアプローチでこの近似方法を正当化する． 重み付きグラフの上でのrandom walkを考えるのである.
$$P_{ij} = \frac{W_{ij}}{\sum_{j'}W_{ij'}} = \frac{W_{ij}}{D_{ii}}$$
によって定義される行列$P=D^{-1}W$である. $\sum_j P_{ij} = 1$で,$P \mathbf{1}=\mathbf{1}$が成立する.よって$P$を重み付きグラフの上でのrandom walkのtransition matrixと考えることが出来る. すなわち,$X(t)$を時刻$t$(ここでは$t$回目の遷移とする)でのrandom walkのstateを表すとすると,
$$P(X(t+1)=j|X(t)=i)=P_{ij}$$
であって，homogeneous Markov chainと考えることが出来る. Markov chainのstateはこの場合グラフのnodeである. Markov chainのErgodic propertyを定義する.

Definition

Markov chain $\{X(t)\}$がergocid
$\Leftrightarrow \exists m \text{ s.t. } \forall t, i,j .\ P(X(t+m)=j|X(t)=i)>0$

erogodicであるとき，$\{X\}$はirreducible かつrecurrentかつstationary distributionをもつ.
stationary distribution $\pi$は$\pi_j = \lim_{m\rightarrow \infty} P(X(t+m)=j|X(t)=i)$である． これまで議論してきた重み付きグラフを上の方法でMarkov chainにするとergodicであり，したがってergodic theoremが成立する．

(以下，講義はもう少し続くが固有値とMarkov chainがどうつながるかわからないので飛ばす．そのうちいい教科書を見つけて読む)

MIT OCW, Machine Learning 13日目

Rohit Singh, Tommi Jaakkola, and Ali Mohammad. 6.867 Machine Learning. Fall 2006. Massachusetts Institute of Technology: MIT OpenCourseWare, https://ocw.mit.edu. License: Creative Commons BY-NC-SA.

停電でデータが消えるという悲しみ

• • • Mixture models and clustering
    • Mixtures and K-means
    • K-means
    • Distance and clustering

Mixture models and clustering

与えられたデータは暗黙的に複数の種類に分けられると仮定し，それを踏まえてより精度の高い推測をするというのがmixture modelの動機のひとつだった. 一方で，その暗黙の構造自体を明らかにすることも有用である. このような問題をclusteringという. つまり，データセットをいくつかのclusterに分類するのである.
mixture modelをgenerative modelとして扱うには，我々が分類しようとしているクラスターがどんなものなのか知らなければならない. 最も単純な例がspherical Gaussian clusterで，すなわち
$$P(\mathbf{x};\theta, m) = \sum_{j=1}^m P(j) N(\mathbf{x};\mu_j,\sigma^2_j I)$$
というmixture modelを推測する.
他にも様々なクラスタリングアルゴリズムがあり,あるものはネストしたクラスターを小さなクラスターをマージしていくことで生成し(hierarchical agglomerative clustering)，またあるものは$D$に最適なクラスターの数を推測してからクラスタリングを行う(k-means). などと期待問題によって適したアルゴリズムは異なる.

データセット$D$に対して$m$をどのように設定すればいいかとか,$D$が十分大きければEM-algorithmでよいクラスタリングが出来るのかとか,頑強なモデルであるのかとか，様々な疑問があり，その答えの一部を以下で与える.

Mixtures and K-means

Gaussian mixture modelを,全ての分散行列を同一のspherical(単位行列の定数倍)にし,さらに全てのcomponentの頻度を同一にすることで単純化する.すなわち
$$P(\mathbf{x};\theta)=\frac{1}{m} \sum_{j=1}^m N(\mathbf{x};\mu_m,\sigma^2 I)$$
を考える. これをEM-algorithmで最適化するとどうなるのかをみる.
まず,クラスター$i, j$の境界がどうなっているかをみる. つまり$P(i |\mathbf{x},\theta)=P(j|\mathbf{x},\theta)$をみたす$\mathbf{x}$をみる. 仮定より,この点で
$N(\mathbf{x}, \mu_i, \sigma^2I)=N(\mathbf{x};\mu_j,\sigma^2I)$が成立する.どちらのGaussianも同じsphericalな共分散行列を持つので, これが成立する$\mathbf{x}$では
$$\|\mathbf{x}-\mu_i\| = \|\mathbf{x}-\mu_j\| \text{ or } 2\mathbf{x}^T (\mu_j-\mu_i)=\|\mu_i\|^2 - \|\mu_j\|^2$$
が成立する.
すなわち境界は線形であり,fig.1のように，任意のクラスターの組に対してこのような境界を引ける. 組ごとの比較はVoronoi partitionを導く. Voronoi partitionのあるregionでは，例えば,全ての点が$\mu_1$に最も近い.このregionは同時に$P(1|\mathbf{x}, \theta)> P(j|\mathbf{x}, \theta)$が任意の$j \neq 1$で成立する.

K-means

上のような単純なモデルではEM-algorithmも単純化できて,それを特にK-meansという.
K-meansでは，E-stepで,$j_t = \arg\min_j \|\mathbf{x}_t-\mu_j\|$とし,M-stepで$\mu_j = average\{\mathbf{x}_t | j_t=j \}$とmeanを設定し直す．

K-meansは非常によく利用されるhard assignment(各点がどれかただ一つのクラスターに分類される)版EM-algorithmである. K-meansはEM-algoと同様初期値が結果に大きく影響するので,初期値を変更して何度も行うのが望ましい. また,ある一点を$\mu_1$に割り当て，$\mu_1$から最も遠い点を$\mu_2$,$\mu_1,\mu_2$から最も遠い点を$\mu_3$,…として初期の$\mu$を決める方法をgreedy packingという.

Distance and clustering

これまでの議論でEuclidean distanceを使ってきたことを正当化する. ところで，多くの場合，特徴データを特別な関数で$\mathbb{R}^n$空間に写像して，それからclusteringを考えたりする．
例えば文書をクラスタリングすることを考える. document $\mathbf{x}$を単語の入った袋と考えて,これを以下の写像によって扱いやすいベクトルにする.
$$\begin{aligned} n_w(\mathbf{x}) &= \text{ number of times world } w \text{ appears in } \mathbf{x} \\ f(w|\mathbf{x}) &= \frac{n_w(\mathbf{x})}{\sum_{w'} n_{w'}(\mathbf{x})} = \text{ term frequencey} \\ \phi_{w}(\mathbf{x}) &=f(w|\mathbf{x}) \cdot \underline{\log \left[ \frac{\text{ number of docs}}{\text{ numer of docw with word }w}\right]}_{IDF} \end{aligned}$$
$\phi(\mathbf{x})=(\phi_{w_1},...,\phi_{w_m})\mathbf{(x)}$をTFIDF(term frequency - inverse document frequency)写像という． IDFは,多くの文書に現れるためクラスタリングに役立たなそうなwordほど小さく(1に近く)なる. こうして文書を実数空間に写して，K-meansのようなアルゴリズムに掛けることができる.
クラスタリングを行う際には適切な距離関数を使うことが非常に重要で，適切な距離を使うためにクラスタリングアルゴリズムを選んでもよいほどである. ほとんどのアルゴリズムは任意の距離関数で使える． 適切な距離関数はモデル選択理論を使って選ぶことが出来る．

MIT OCW, Machine Learning 12日目

Rohit Singh, Tommi Jaakkola, and Ali Mohammad. 6.867 Machine Learning. Fall 2006. Massachusetts Institute of Technology: MIT OpenCourseWare, https://ocw.mit.edu. License: Creative Commons BY-NC-SA.

モデル選択理論難しすぎ

• • Mixture models
    • • Example: Student exam model: 1-year
      • Example: student exam model: K-years
  • Collaborative filtering
  • Estimating mixtures: the EM-algorithm (期待値最大化法)
    • Complete data
    • Imcomplete data
      • Algorithm (EM)
      • Example

Mixture models

mixture model(混合モデル)は与えられたデータの曖昧さを捉えるモデルで，データの背後に有る，観測できない要因についての仮定を行う. 観測された一つのexampleを$\mathbf{x}$というベクトルで表すとする. exampleは$m$個の要因($1,...m$とする)のどれかによって生成されている$m$をcomponentの数という． $j \in \{1,..m\}$その要因であるとすると,$\mathbf{x}$の事後確率は$P(\mathbf{x}|j)$である. また$j$の頻度を$P(j)$とすると,$P(\mathbf{x}, j)=P(j)P(\mathbf{x}|j)$. 実際の$j$が何であるかは一般にはわからず，全ての$\{1, ..., m\}$について混合して，$\mathbf{x}$の確率
$$P(\mathbf{x}) = \sum_{j=1}^m P(\mathbf{x}|j)P(j)$$
となる.

Example: Student exam model: 1-year

例えば,学生たち$\{1,...,n\}$の試験の結果$D_1=\{\mathbf{x}_1,...\mathbf{x}_n\}, \mathbf{x_i}=(\text{問1の点数, 問2の点数},...)$をモデル化することを考える. 学生たちは，例えば学士での専攻のような，$D$では与えられていない要因によってことなった正答/誤答の傾向が存在すると仮定する. そのような要因が合計で$m$個(この$m$を選ぶのはmodel selectionの問題である)あって，さらに個々の学生がどれに該当するかわからないときのモデリングを考える.
それぞれの学生の点数が独立とするなら
$$P(\mathbf{x_1,...,x_n}|\theta)=\prod_{t=1}^n \left[\sum_{j=1}^m P(\mathbf{x}_t|j)P(j) \right]$$ である.

Example: student exam model: K-years

上の例で,過去$K$年間のデータがあるとする. $k$年での学生数$n_k$で,$\mathbf{x}_{k,t}$は学生$t$の$k$年目の試験結果とする($t$はただのインデックスで,$t$が同じだからといって同じ学生であるというわけではない). $m$と$P(\mathbf{x}|j)$は変わらないと仮定する. しかし学生の数$n_k$は各年でことなって,$j$の頻度$P(j)$も一定でなく,$P(j|k)$と条件付きにする. この場合のmixture modelは
$$P(\mathbf{x}|k, \theta) = \sum_{j=1}^m P(\mathbf{x}|\theta_j)P(j|k)$$
そして全てのデータ$D=\{D_1, ..., D_k\}$を考えたときの尤度は
$$L(D;\theta)=\prod_{k=1}^K\prod_{t=1}^{n_k} P(\mathbf{x}_{k,t}|k,\theta)=\prod_{k=1}^K\prod_{t=1}^{n_k} \left(\sum_{j=1}^m P(\mathbf{x}_{k,t}|\theta_j)P(j|k) \right)$$
となる.ここでの$\theta$は$\{\theta_j\},\{P(j|k)\}$をも決定する.

Collaborative filtering

mixture modelは推薦システムにもよく使われる. $n$人のユーザに$m$本の映画を推薦する問題を考える. ユーザは$m$のうち極わずかだけに点数をつけているとして,つけていない映画たちをどう評価するかを推測するのが我々の課題である. このような問題をcollaborative filtering(協調フィルタリング)という.
点数は$r_{ij} \in \{1, ...,5\}$をつけられるとする. ただし$r_{ij}$はユーザ$i$の映画$j$に対する評価とする. ユーザたちが実際に与えた評価を$D$とする. $r_{ij}$が与えられているとき$r_{ij}\in I_D$と書く．
collaborative filteringでは,ユーザと映画の両方にいくつかの種類があって,それが評価に影響すると仮定する.すなわち，それぞれの映画が”movie types” $z_m \in \{1,..,K_m\}$の分布の上にあって,ユーザも”user types” $z_u\in \{1,...,K_u\}$の分布の上にあるとする. 有る映画が,すべてのユーザにとって同じタイプであるとは考えず,それぞれの映画が，その映画に対応した特徴のバッグをもっており，それぞれのユーザごとにそのバッグからタイプを取り出すと考える. この仮定はユーザにも適用される． すなわち点数を付けるたびに，そのユーザのタイプのバッグからタイプが取り出される.
$r_{ij}\notin I_D$を以下によって推測する.
$P(z_m|j)$から映画$j$のタイプをサンプルし,また$P(z_j|i)$からユーザ$i$のタイプをサンプルする. さらに$P(r_{ij}|z_u, z_m)$から$r_{ij}$をサンプルするのである. これを全ての$z_m, z_u$に足し合わせて
$$P(r_{ij}|i, j, \theta)=\sum_{z_u=1}^{K_j}\sum_{z_m=1}^{K_m}P(r_{ij}|z_u,z_m)P(z_u|i)P(z_m|j)$$
となる. $\theta$はタイプから評価への写像$\{P(r|z_u, z_m)\}$と$\{P(z_u|i)\}, \{P(z_m|j)\}$を決定する.
$D$を与えられたときの尤度は
$$L(D;\theta) = \prod_{(i,j)\in I_D} P(r_{ij}|i,j,\theta)$$
である.
さらに,ユーザの評価のスタイルもモデルに組み込める. 例えば$3,4,5$のような高評価に偏った評価をする人や,$1$と$5$のみのような極端な評価をする人を考えることが出来る.このような評価スタイルの集合を$\{1,...,K_s\}$とする.ユーザのスタイルは全ての映画に一貫しているが，個々のユーザにどうスタイルを割り当てるかは未知とする. ユーザがスタイル$s \in \{1,...,K_s\}$をもつ確率は$P(s)$と書ける. スタイルも$\{1,..,K_s\}$すべてを$PS(s)$を重みにして総和を考えて尤度を求めるとすると,尤度$L'$は,
$$L'(D;\theta) = \prod_{i=1}^n \left[\sum_{s=1}^{K_s} P(s) \underline{\prod_{j: (i,j)\in I_D} \left( \sum_{z_u=1}^{K_u} \sum_{z_m=1}^{K_m}P(r_{ij}|z_u,z_m,s)P(z_u|i)P(z_m|j) \right)}_{(1)} \right]$$
となる.(1): user $i$がスタイル$s$によって評価する尤度
このモデルは
$$\underline{ (K_s-1)}_{P(s)} + \underline{(5-1)K_uK_mK_s}_{P(r|z_u,z_m,s)}+\underline{n(K_u-1)}_{P(z_u|i)} + \underline{m(K_m-1)}_{P(z_m|j)}$$
個のパラメータを持つ.
さらに充実したモデルでは,”missing elements”のモデル，すなわちある映画の評価がなぜなされないかもモデル化するはずである.

Estimating mixtures: the EM-algorithm (期待値最大化法)

midture modelの例をいくつか見てきた. データによく合うようにパラメータを設定する方法を論じる. $\mathbf{x}$の要因$j$が不明なので，$\{1,..,m\}$で総和を取ってきたのだが,まずは要因がわかっているモデルを考える．

Complete data

$$P(\mathbf{x}; \theta) = \sum_{j=1}^m P(j)N(\mathbf{x};\mu_j,\Sigma_j)$$
それぞれの$\mathbf{x}_t$に対応する$j_t$が既知であると仮定して議論する. $\delta(j|t) =\begin{cases} 1 \ \ (j = j_t) \\ 0 \ \ (j \neq j_t) \end{cases}$を使うと便利である． log-likelihoddは
$$\begin{aligned} l(\mathbf{x_1,...,x_n},j_1,...,j_n;\theta) &= \sum_{t=1}^n \log [P(j_t)N(\mathbf{x}; \mu_{j_t},\Sigma_{j_t})] \\ &= \sum_{t=1}^n \sum_{j=1}^m \delta(j|t) \log [P(j)N(\mathbf{x}_t; \mu_j, \Sigma_j)] \\ &= \sum_{j=1}^m (\sum_{t=1}^n \delta(j|t)) \log P(j) + \sum_{j=1}^m (\sum_{t=1}^n \delta(j|t) \log N(\mathbf{x}_t; \mu_j, \Sigma_j)) \end{aligned}$$
尤度を最大とするパラメータをハットで表すと,
$\hat{P}(j) = \frac{\hat{n}(j)}{n}, \ \ \hat{n}(j) = \sum_{t=1}^n \delta(j|t)$
$\hat{\mu}_j = \frac{1}{\hat{n}(j)} \sum_{t=1}^n \delta(j|t)\mathbf{x}_t, \ \ \hat{\Sigma}_j = \frac{1}{\hat{n}(j)} \sum_{t=1}^n \delta(j|t)(\mathbf{x}_t-\hat{\mu_j})(\mathbf{x}_t-\hat{\mu}_j)^T$
となる.このように$\{j_t\}$が既知である場合には，最尤推定は簡単に行えるとわかる.

Imcomplete data

$j_t$がわかっていない場合を考える. $\theta^{(l)}$を初期のパラメータとする. このパラメータで,ある$\mathbf{x}_t$が$j$によって生成される確率は
$$P(j|\mathbf{x}_t,\theta^{(l)})= \frac{P^{(l)}(j)N(\mathbf{x}_t; \mu^{(l)}_j, \Sigma^{(l)}_j)}{\sum_{j'=1}^m P^{(l)}(j')N(\mathbf{x_t}; \mu^{(l)}_{j'}, \Sigma^{(l)}_{j'})}=\frac{P^{(l)}(j)N(\mathbf{x}_t;\mu_j^{(l)},\Sigma_j^{(l)})}{P(\mathbf{x}_t; \theta^{(l)})}$$
$\delta(j|t)$という二値の割当の代わりに,$p^{(l)}(j|t) = P(j|\mathbf{x}_t, \theta^{(l)})$という”soft”な割当を使うのである. この割当は$\theta^{(l)}$によっており,$\theta$を更新していくたびに変化していく.
これらの結果から,Expectation Maximization algorithm (EM)が導かれる. EMは全てのmixture modelと更に広範なモデルに適用できる. Gaussian mixtureでのEM-algorithmは以下の通り.

Algorithm (EM)

(step1)
$\theta^{(0)}$を定める. 例えば$P^{(0)}(j)=1/m$とし,$\mu^{(0)}_j$をランダムに選んだ$D$の点に,$\Sigma_j^{(0)}$を$D$の分散行列としたりなどする.
(E-step)
$p^{(l)}(j|t) = P(j|\mathbf{x}_t, \theta^{(l)})$を$\theta^{(l)}$によって評価する.
(M-step)
パラメータを，
$$\begin{aligned} P^{(l+1)}(j) &= \frac{\hat{n}(j)}{n}, \ \ \hat{n}(j)=\sum_{t=1}^n p^{(l)}(j|t) \\ \mu_j^{(l+1)} &= \frac{1}{\hat{n}(j)} \sum_{t=1}^n p^{(l)} (j|t) \mathbf{x}_t \\ \Sigma_j^{(l+1)} &= \frac{1}{\hat{n}(j)}\sum_{t=1}^n p^{(l)} (j|t) (\mathbf{x}_t - \mu^{(l+1)}_j)(\mathbf{x}_t - \mu_j^{(l+1)})^T \end{aligned}$$
によって更新する.

この更新則によってlog-likelihoodは増加し,またパラメータは収束することが証明されているが, その極限では$d/d\theta l(D;\theta)=0$が成立することしか保証されていない.

Example

2つのGaussianのmixture modelを考える. fig.2 はEM-algorithmのイテレーションの様子である.

MIT OCW, Machine Learning 11日目 宿題3

Rohit Singh, Tommi Jaakkola, and Ali Mohammad. 6.867 Machine Learning. Fall 2006. Massachusetts Institute of Technology: MIT OpenCourseWare, https://ocw.mit.edu. License: Creative Commons BY-NC-SA.

assigmnemt 3
Q and A

1.

答案.

(b) $E[error_{LOOCV}(S_n)]=E[\frac{1}{n}\sum_t error_t(S_n)] = \frac{n}{n} \cdot E[(y-\hat{f}_{S_{n-1}}(\mathbf{x}))^2]=E[(y-\hat{f}_{S_{n-1}}(\mathbf{x}))^2]$
(c) $$\begin{aligned}var[error_{LOOCV}(S_n)] &= var[\frac{1}{n} (error_1(S_n) + \cdots+error_n(S_n))] \\ &=\frac{1}{n^2}var(\sum_1^n error_i(S_n)) <_{(1)} var(error_1(S_n)) \\ &= E[(y-\hat{f}_{S_{n-1}}(\mathbf{x}))^2] \end{aligned}$$
(1)の不等号を示せなければならなのだが,模範解答でも定性的に言及されただけだからもう明らかでいいと思う
(d)
$f^k_{keep}$がtraining errorを0にするというのは，任意の$t\in\{1,..,n\}$で$y_t = x^{(t)}_r$が成り立つということ. $y_t$を生成する$Y$と$x_r$を生成する$X_r$は独立で,$P(Y=1)=P(X_r=1)=0.5, P(Y=-1)=P(X_r=-1)=0.5$だから,$f^{k}_{keep}$がtraining errorを0にする確率は$P(\forall t. Y=X_r)=_{(1)}\prod_t P(Y=X_r)=1/2^n$. (1): 各サンプルの生成の独立性
$f^k_{flip}$も同様で,足し合わせると求める確率$2^{-(n-1)}$が得られる.
(e)
$\mathcal{M}_r$において$f^r_{keep}$のtraining error $\epsilon << 1/2$とする.
$f^r_{keep}$の$error_i(S_n)$を考える($i = 1,..., n$)
$\epsilon << 1/2$だから，training setから$i$番目を引いても$\mathcal{M}_r$から選ばれるestimatorは変わらず.$f^r_{keep}$のまま. したがって$\hat{f^r}_{-i} = f^r_{keep}$が任意の$i$で成立.
よって$error_{LOOCV}(S_n) = (1/n) \cdot \sum_i (y_i - f^r_{-i}(x_i))^2 = (1/n)\cdot\sum_i (y_i-f^r_{keep}(x_i))^2$
これは$f^r_{flip}$のtraining errorが$\epsilon << 1/2$の時も同じ. よって示せた.

模範解答.

(a)
r.v. $A, B$が同じdistributionをもつとき，$E[f(A)]=E[f(B)]$であるのを利用する.これは
$$E[f(A)] = \int f(x)p_A(x)dx = \int f(x)p_B(x)dx = E[f(B)]$$
からわかる.
$A,B$がそれぞれr.v.の集合であっても成立する. $A=\{S^{-1}_n, (\mathbf{x}_1, y_1)\},\ B=\{S_{n-1}, (\mathbf{x}, y)\}$とする.ただし$S_n^{-1}$でtrainし，$(\mathbf{x}_1, y_1)$を識別子, $S_{n-1}$は$n-1$個のtraining dataで$(\mathbf{x}, y)$を識別する. $A,B$は同じdistributionを持つから,与えられた四季が成立する.
(f)
training error を$\delta$とすると,classifierは$n\delta/4$回間違える. ある次元$i$においてtraining errorが$\epsilon$以下である時,すなわち間違いがせいぜい$floor(n\epsilon/4)$であるとする.間違いの回数を$k$とおくと,間違いの起こる場合の数は$nCk$通りで,まさにそこで間違いが起こる確率は$2^{1-n}$. よってtraining errorが$\epsilon$未満である確率は
$$p = \sum_{k=0}^{floor(n\epsilon/4)} nCk \frac{1}{2^{n-1}}$$
errorが$\epsilon$以上である確率は$1-p$で,$d$次元全てがそうである確率は$(1-p)^d$.これが$1/2$以下であれば少なくとも1つの次元でerrorが$\epsilon$未満となる. よって
$(1-p)^d \leq 1/2$を解くと,
$$d \geq \frac{1}{\log_2 \frac{1}{1-p}}$$

2.

答案.

(a)
$$P(S_n|\{l\}) = \sum_{\theta \in \{-1, 1\}} 2^{-1} \prod_{t=1}^n \left[ \frac{1+y_t\theta_l x_{t_l}}{2} \right]=\frac{1}{2^{n+1}} \left[\prod_{t=1}^n (1+y_tx_{t_l})+\prod_{t=1}^n(1-y_tx_{t_l}) \right]$$
(d) marginal likelihoodが減少し始めるとき

模範解答.

(b) 与えられた式は間違いに対して確率0を割り当ててしまう.
$$P(S_n|\mathcal{J})=\sum_{\theta \in \{1, -1\}^{|\mathcal{J}|}}2^{-|\mathcal{J}|}\prod \left[\frac{1}{|\mathcal{J}|}\sum_{j \in \mathcal{J}} f(y_t\theta_j , x_{tj}) \right]$$
とする.

MIT OCW, Machine Learning 10日目 モデル選択の理論1

Rohit Singh, Tommi Jaakkola, and Ali Mohammad. 6.867 Machine Learning. Fall 2006. Massachusetts Institute of Technology: MIT OpenCourseWare, https://ocw.mit.edu. License: Creative Commons BY-NC-SA.

Lecture 9

Kernel Optimization

kernelのあるパラメータを変えて,問題により適したkernelをつくることができる. 例えばradial basis kernelの$\beta$のようなパラメータを変化させたり,$\mathbf{x}$の次元に重み付けをしてから$\phi$に渡すような方法が考えられる. パラメータのよさの基準には,cross-validationやgeneralization errorに関連した基準(marginなど)が用いられる. marginは$\phi$を定数倍すると同時に倍化するため,normalization $\|\phi(\mathbf{x})\|=1$という制限を加える.normalizationは例えば
$$\tilde{K}(\mathbf{x}, \mathbf{x'})=\frac{K(\mathbf{x, x'})}{\sqrt{K(\mathbf{x,x'})K(\mathbf{x,x'})}}$$
で実現できる.
他のkernel optimizationの方法にkernel alignentがある. すなわち,パラメータやGram matrixを理想的なkernelに近づけるように調整するのである. 例えばclassificationでは
$$K^*_{ij}=y_iy_j$$
を標的となるkernelのGram matrixとする.というのは,$\alpha_j = 1/n$とすれば,
$$\sum_{j=1}^n \alpha_j y_j K^*_{ij}=y_i$$
と,全てのtraining exampleが等しいmarginで正しく分類できるためである.
kernelをこの標的に近づける方法を考える.
$$K(\mathbf{x}, \mathbf{x'};\theta) = \sum_{i=1}^m \theta_i K_i(\mathbf{x,x'}), \theta_i \geq 0, \sum_{i=1}^m \theta_i=1$$

のように,kernelたちのconvex combinationによってkernel $K$を構成するとき,$\theta_i$が我々が選べるパラメータである. $K$のGram matrix $K_{ij}(\phi)$を,標的のGram matrix $K^*_{ij}$に近づけるため,Gram matrixをベクトルと考えて,その内積を
$$<K^*, K_\theta> = \sum_{i,j=1}^n K^*_{ij}K_{ij}(\theta)$$
と定める. こうして$\theta$は$K^*$と$K(\theta)$のcosine類似度
$$\frac{<K^*, K_\theta>}{\sqrt{<K^*,K^*><K_\theta,K_\theta}}$$
を最大化させる$\theta$を求めれば良い.

Model (kernel) selection

少ないtraining exampleに複雑すぎるmodel(kernel)を使うと,over-fittingという問題が起きる. 問題によって使うkernelの種類を制限することがある. kernelを選ぶことで
linearな$K_1$があるとき,discriminant functionは
$$f_1(\mathbf{x}; \theta, \theta_0) = \theta^T \phi^{(1)}(\mathbf{x})+\theta_0$$
という形をしている.$\phi^{(1)}(\mathbf{x})$は$K_1(\mathbf{x, x'})=\phi^{(1)}(\mathbf{x})^T\phi^{(1)}(\mathbf{x'})$となる関数で,$\mathbf{x}$の$K_1$によるfeature representationという. $\theta, \theta_0$を変えることで可能なdiscriminant functionの集合
$$\mathcal{F}_1 = \{f_1(\cdot; \theta, \theta_0): \theta \in \mathbb{R}^d_1, \theta_0 \in \mathbb{R}\}$$
を構成できる. 同様にquadratic kernelによって可能な集合$\mathcal{F}_2$がある. このように

Model Selection Preliminaries

$S_n = \{(\mathbf{x}_1, y_1)...,(\mathbf{x}_n,y_n)\}$はtraining setとする. $\mathcal{F}_i$をmodelとして選んで,$\hat{f}_i \in \mathcal{F}_i$をbest fitting discriminant functionとすると,$\hat{f}_i$は
$$J(\theta, \theta_0) = \sum_t Loss(y_t, f(\mathbf{x}_t; \theta, \theta_0))+\lambda_n \|\theta\|^2$$
を最小化する.$Loss$はhinge lossでもlogisticでも他の何でもよい. $\lambda_n$は$n$によってへｋ擦るregularization parameterである. $\hat{f}_i=f(\mathbf{x};\hat{\theta}, \hat{\theta_0})$が新しいexampleにどれほどgeneralizeできているかが問題となる.
それぞれの$(\theta,\theta_0)$すなわちそれぞれのdiscriminant functionはexpected lossあるいはrisk
$$R(\theta,\theta_0) = E_{(\mathbf{x},y)\sim P}\left\{Loss^* (y, f(\mathbf{x};\theta,\theta_0)) \right\}$$
をもつ.ここで$P$は問題となるデータを生成している分布で，普通は未知であり,$(\mathbf{x},y)$もそこから生成されていると考える. これが,我々が最小化したいgeneralization errorである. $S_n$によって決まる$\hat{f}_i$のrisk $R(\hat{f}_i)$を最小化する$\mathcal{F}_i$を選ぶことが最終的な目標である. ただし$S_n$は$P$から生成されるので,$R(\hat{f}_i)$も$\hat{f_i}$も確率変数である(理論的には便利な仮定だが,実際に$S_n$が正しく$P$から生成されているとは限らない).
$P$が既知であるなら$argmax_y P(y|\mathbf{x})$を考えれば良いが，ここでは$P$は未知として,$S_n$だけを使って$\hat{f}_i \in \mathcal{F}_i$を，さらには$\mathcal{F}_i$をも選ばなければならない.
簡単のため,$\mathcal{F}_1, \mathcal{F}_2$を，linearとquadraticなdiscriminant functionの集合とし,$\mathcal{F_1, F_2}$のみを議論する. $\mathcal{F}_1 \subset \mathcal{F}_2$だから,$\mathcal{F}_2$から選ぶことで必ずtraining setにおけるerrorが小さい$f$を得られるが,example とlabelの関係が線形であるときにも非線形な$\mathcal{F}_2$から選ぶと，over-fittingしているかもしれない. 真の分布が線形分離可能であるとき,quadraticなdecison boundaryはノイズに影響されてgeneralizeがうまく行っていないということである. したがって$\mathcal{F}$が複雑になるほどtraining setに対する性能が向上する一方でtest setに対する性能は低下していく(fig.1). よって適切な複雑さを選ぶことが重要になってくる.

Model selection criteria: structural risk minimization

expected risk
$$R(\hat{f}_i) = E_{(\mathbf{x}|y)\sim P}\left\{ Loss^* (y, \hat{f_i}(\mathbf{x})) \right\}$$
とempirical risk(training errro)
$$R_n(\hat{f}_i) = \frac{1}{n} \sum_{t=1}^n \left( Loss^* (y, \hat{f_i}(\mathbf{x})) \right)$$
を関連付けることができれば,$R_n(\hat{f}_i)$を計算することで$R(\hat{f}_i)$を議論することが出来る. モデルが複雑になるほどtraining errorがgeneralization errorを表現しなくなっていくと考えられるので,$R_n$と$R$の関係を以下のように記述する.
$$R(\hat{f}_i) \leq R_n(\hat{f_i}) +C(n, \mathcal{F}_i, \delta) \ \ \ \ (16)$$
$C$はcomplexity penaltyといって,$\mathcal{F}_i$が複雑になるほど増大し,$n$によって減少する.
(16)はupper bound guarantee of generalization errorを与える. このupper boundが最小になるような$\mathcal{F}_i$を選べば良い. fig.2 はモデルの複雑さとこのboundの関係である.

$\mathcal{F}_i$が有限集合である時の不等式(16)の意味を考える.
$$P(\max_{f\in\mathcal{F}_i} |R(f)-R_n(f)|>\epsilon) \leq \delta$$
の上限を見積もる. これは少なくとも1つの$f$について，そのtraining errorとriskの差が$\epsilon$を上回る確率で,sample spaceは$S_n$の選び方である.
$\delta = P(\max_{f \in \mathcal{F}_i} |R(f)-R_n(f)|>\epsilon) \ \ (6)$は
$$R(f) \leq R_n(f) + \epsilon \ \ \text{for all } f \in \mathcal{F}_i$$
という主張が成立しない確率と言える. $\delta$を固定すると,(6)をみたす最小の$\epsilon =\epsilon(n, \mathcal{F}_i, \delta)$がcomplexity penaltyとなる.
$(6)$によって$\delta$を計算することはふつう不可能だから，上限を与える.
$$\begin{aligned}P(\max_{f \in \mathcal{F}_i} |R(f)-R_n(f)|>\epsilon)&=P(\exists f : |R(f)-R_n()|>\epsilon) \\ &\leq \sum_{\mathcal{F_i}} P(|R(f)-R_n(f)|>\epsilon)\ \ \ (8)\end{aligned}$$
$f$を固定して$P(|R(f)-R_n(f)|>\epsilon)$を考える. training sample $(\mathbf{x}_t, y_t)$がi.i.d.に得られて,$s_t = \begin{cases} 1 \ \ &\text{ if } y_tf(\mathbf{x}_t)\leq 0 \\ 0 &\text{otherwise}\end{cases}$とすると empirical error $R_n(f)$は$s_t$の和で,
$$R_n(f) = \frac{1}{n}\sum_{t=1}^n s_t$$
$E[s_t]=R(f)$だから,
$$P(|R(f)-R_n(f)|>\epsilon) = P(|q-\frac{1}{n}\sum_t s_t|>\epsilon)$$
ただし$q=R(f)$で,確率のsample spaceは$P(s_t=1)=q$をみたす$s_1, ..., s_n$である.
Hoeffding’s inequalityから
$$P(|q-\frac{1}{n}\sum_{t=1}^n s_t| > \epsilon)\leq 2 \exp(-2n\epsilon^2)$$
が成立する. この上限は$f$によらない. この結果を(8)に代入して，
$$P(\max_{f \in \mathcal{F}_i}|R(f)-R_n(f)|>\epsilon) \leq 2|\mathcal{F}_i|\exp(-2n\epsilon^2)=\delta$$
が成立する. $\epsilon$に解いて,
$$\epsilon=\epsilon(n,\mathcal{F}_i, \delta) = \sqrt{\frac{\log|\mathcal{F}_i|+\log(2/\delta)}{2n}}$$
である.これが$\mathcal{F}_i <\infty$の場合のcomplexity penaltyである.
以上より,少なくとも$1-\delta$の確率で
$$R(f) \leq R_n(f) + \sqrt{\frac{\log|\mathcal{F}_i| + \log (2/\delta)}{2n}}, \text{ uniformly for all }f \in \mathcal{F}_i$$
が成立する. model selectionでは$\{\mathcal{F}_i\}$のそれぞれについて$\hat{f_i}$を選び，$\hat{f}_i, |\mathcal{F}_i|$によってboundを計算し,boundが最小となる$\mathcal{F}_i$を選ぶ． このとき$n$と$\delta$は固定する．

Example

$\delta=0.05$とし,training error 0, generalization error が最大10%であるようにtraining exampleの個数$n$を見積もる.
$$R(f) \leq 0 + \sqrt{\frac{\log |\mathcal{F}_i| + \log (2/0.05)}{2n}}\leq 0.10$$
だから,
$$n = \frac{\log|\mathcal{F}_i| + \log (2/0.05)}{2(0.10)^2}$$
である.

Model selection criteria: Bayesian score, Bayesian information criterion

linear regressionの例を通じてBayesian scoreについての理解を深める. モデル$\mathcal{F}$は$d$次元のインプット$\mathbf{x}$を$y \in \mathbb{R}$に写す写像で,
$$P(y|\mathbf{x}, \theta, \sigma^2) = N(y; \theta^T \mathbf{x}, \sigma^2)$$
とする. $\sigma^2$を固定して,$\theta$だけを動かすとする. $D=\{(\mathbf{x}_1, y_1),...,(\mathbf{x}_n, y_n)\}$が与えられたとき,likelihoodは
$$L(D;\theta) = \prod_{t=1}^n N(y_t; \theta^T\mathbf{x}_t,\sigma^2) = \prod_t \frac{1}{\sqrt{2\pi \sigma^2}}\exp(-\frac{1}{2}(y_t-\theta^T\mathbf{x}_t)^2)$$
以前は$L$を最大化する$\hat{\theta}$を唯一つ選んだが，Bayesian analysisではlinear regression functionたちを$L(D;\theta)$によって重み付けして，それら全てを利用する.
このような枠組みでは,$D$を得た後の$\theta$の知識はposterior distribution $P(\theta|D)$であって,これは$L(D;\theta)$と相似である.つまり$P(\theta|D) \propto L(D;\theta)$.
しかし例えば$D=\phi$の場合には$\forall \theta. L(D;\theta)=1$だから,$P(\theta|D)$が発散してしまう．　よってprior distribution $P(\theta)$を導入する.
$$P(\theta) = N(\theta; 0, \sigma^2_P \cdot I)$$
すると
$$P(\theta|D) \propto L(D;\theta) P(\theta)$$
で,normalization constantは
$$P(D|\mathcal{F}) = \int L(D;\theta)P(\theta)d\theta$$
であり,marginal likelihoodともいう. これは$\mathcal{F}$と$D$にのみよる. regressionでは
$$\begin{aligned} \log P(D|\mathcal{F}) &= -\frac{n}{2} \log(2\pi\sigma^2) + \frac{d}{2} \log \lambda - \frac{1}{2} \log |\mathbf{X^TX}+\lambda I| \\ &-\frac{1}{2\sigma^2}(\|\mathbf{y}\|-\mathbf{y^TX}(\mathbf{X^TX}+\lambda I)^{-1}\mathbf{X^ty})\end{aligned}$$

ここで$\lambda = \sigma^2/\sigma^2_P$はnoise とpriorの比で,$\mathbf{X}=[\mathbf{x}_1,...,\mathbf{x}_n]^T, \mathbf{y}=[y_1,...,y_n]^T$である.
このときposteriorは
$$P(\theta|D) = \frac{L(D;\theta)P(\theta)}{P(D|\mathcal{F})}$$
と正規化される.$P(\theta|D)=N(\theta;\mu,\Sigma)$とposteriorも正規分布する.
$$\begin{aligned} \mu = (\mathbf{X^TX}+\lambda I)^{-1}\mathbf{X^Ty} \\ \Sigma = \sigma^2 (\mathbf{X^TX}+\lambda I)^{-1} \end{aligned}$$

新たな$\mathbf{x}$に対する推測は
$$P(y|\mathbf{x},D) = \int P(y|\mathbf{x},\theta)P(\theta|D)d\theta$$
で与えられる. 真のBayesianはまさに全ての$\theta$について上の積分を行うが,我々はfeature mapping $\mathbf{x} \mapsto \phi(\mathbf{x})$で特徴づけられるregression modelに$\theta$を制限して議論することになる.linearな$\phi^{(1)}$とquadraticな$\phi^{(2)}$をfeature mappingとする.
$$\begin{aligned} \mathcal{F}_1: \ \ &P(y|\mathbf{x},\theta,\sigma^2) = N(y;\theta^T\phi^{(1)}(\mathbf{x}),\sigma^2), \theta \in \mathbb{R}^{d_1}, P(\theta|\mathcal{F}_1) \\ \mathcal{F}_2: &P(y|\mathbf{x},\theta,\sigma^2)=N(y;\theta^T \phi^{(2)}(\mathbf{x}),\sigma^2) , \theta \in \mathbb{R}^{d_2}, P(\theta|\mathcal{F}_2) \end{aligned}$$
が比較するmodelである. modelにPrior distribution $P(\theta|\mathcal{F})$を含むのには利点も欠点もあるが，どちらにせよ含まないのと大した差はない.
$\mathcal{F_1, F_2}$のうち,よりmarginal likelihood (Bayesian score)が大きい方を選ぶことになる. すなわち,$D$を与えられたら,$P(D|\mathcal{F}_i) > P(D|\mathcal{F}_j)$ならば$\mathcal{F}_i$を選ぶのである.

Model selection criteria: Bayesian information criterion(BIC)

Bayesian information criterion(BIC)はBayesian scoreに対するasymptotic(漸近的な) 近似であって，その単純さのためによく使われる.
$$BIC = l(D,\hat{\theta}) - \frac{d}{2}\log (n)$$
である.ここで$l(D;\theta)$はtraining dataに対するmaximum likelihoodの対数であって,$d$はmodelのindependent parameterの個数, $n$はtraining exampleの個数である. $BIC$は$n$が十分大きいときBayesian scoreに漸近する. Bayesian scoreの計算は困難なことが多いので,かわりにBICを使う. Bayesian scoreと同様に,BICが大きい方のmodelを選ぶ.

MIT OCW, Machine Learning 09日目 カーネル化SVM

Rohit Singh, Tommi Jaakkola, and Ali Mohammad. 6.867 Machine Learning. Fall 2006. Massachusetts Institute of Technology: MIT OpenCourseWare, https://ocw.mit.edu. License: Creative Commons BY-NC-SA.

Lecture 8

Support Vector Machine Revisited

SVMをdual form(exampleが内積でのみ現れる形)に変換する. すべてのexampleを$\phi$で$d$次元のfeature spaceに写し,$\{\phi(\mathbf{x_t}, y_t)\}_{t=1}^n$が線形分離可能であるようにし,feature spaceにおいてmarginを最大化するパラメータを考える.この問題は
$$\text{minimize } \|\theta\|^2/2 \text{ subject to } y_t(\theta^T \phi(\mathbf{x}_t) + \theta_0) \geq 1, t=1,...,n \ \ \ (1)$$
という最適化問題に一致する. もちろんslack variableも導入できるが,これは後に回す. このような最適化問題(凸,線形制約)は,Lagrange multipliersによってdual formに変形できる. $\alpha_t \geq 0$を導入し,$\alpha = \{\alpha_1,...,\alpha_n\}$によって
$$J(\theta, \theta_0;\alpha)=\|\theta\|^2/2 - \sum_{t=1}^n \alpha_t \left[y_t(\theta^T\phi(\mathbf{x}_t)+\theta_0)-1 \right]$$
を$\alpha$によって最大化することを考えるのである.$J(\theta, \theta_0)=\max_{\alpha\geq 0} J(\theta, \theta_0, \alpha)$の最小化が$(1)$に一致することを示す.
$\theta, \theta_0$を少なくとも1つの束縛条件が満たされていないように設定する.$y_i(\theta^T \phi(\mathbf{x}_i)+\theta_0)<1$であるとすると任意の$\alpha_i>0$に$-\alpha_i[y_i(\theta^T \phi(\mathbf{x}_i)+\theta_0)-1]>0$.$\alpha_i =\infty$とすれば$J(\theta,\theta_0)=\infty$.だから,Lagrange multiplier $\alpha$は制約条件を満たさせる働きがあるとわかる.
Slater conditionsという条件を満たしているとき,ある変数で最大化し,他の変数で最小化するというLagrange multipliersの最適化問題の最大化最小化の順序を交換できる.つまり
$$\min_{\theta, \theta_0} \max_{\alpha\geq 0} J(\theta, \theta_0;\alpha) = \max_{\alpha\geq 0} \min_{\theta, \theta_0} J(\theta, \theta_0, \alpha)$$
である. 左辺をprimal formといい,右辺をdual formという. dual formについて,まず$\min_{\theta, \theta_0}J$を解く.微分して
$$\begin{aligned} \frac{d}{d\theta_0}J &= - \sum_{t=1}^n \alpha_t y_t =0\\ \frac{d}{d\theta} J &= \theta - \sum_{t=1}^n \alpha_t y_t \phi(\mathbf{x}_t)=0 \end{aligned}$$
またしても,最適な$\theta$は$\{\phi(\mathbf{x}_t)\}_t$の張る空間の元となった.これらをもとの式に代入して,
$$\begin{aligned} J(\alpha) &= \min_{\theta,\theta_0}J(\theta, \theta_0,\alpha) \\ &= \begin{cases} \sum_t \alpha_t - (1/2) \sum_i \sum_j \alpha_i \alpha_j y_iy_j [\phi(\mathbf{x}_i)^T \phi(\mathbf{x}_j)], &\text{ if } \sum_t \alpha_t y_t = 0 \\ -\infty &\text{otherwise} \end{cases} \end{aligned}$$
よって,dual formの解は
$$\begin{aligned} \text{maximize } &\sum_t \alpha_t - (1/2) \sum_i \sum_j \alpha_i \alpha_j y_iy_j [\phi(\mathbf{x}_i)^T \phi(\mathbf{x}_j)] \\ \text{subject to } & \alpha_t \geq 0, \sum_t \alpha_t y_t = 0\end{aligned}$$
の解である. これがSVMのdual formとかkernel formといい,quadratic optimization problemであり,Gram matrix $\mathbf{K} = (k_{i,j}) = (\phi(\mathbf{x}_i)^T \phi(\mathbf{x}_j))$によって,特徴づけられる.
maximum margin hyperplaneはsupport vectorと呼ばれる少数のexampleによって決まることをすでに見たが,これは$\phi$によって写像されたexampleたちにも同様で,ほとんどの$\hat{\alpha}_t$は$0$になり,$\hat{\alpha_t}>0$なるとき,$\mathbf{x_t}$や$\phi(\mathbf{x_t})$をまたsupport vectorという.
$\hat{\alpha}_t$が決まると,$SV$をsupport vectorの集合として,
$$\begin{aligned} \hat{y}(\mathbf{x}) &= \hat{\theta}^T\phi(\mathbf{x})+\hat{\theta_0} \\ &= \sum_{t} \hat{\alpha_t}y_t [\phi(\mathbf{x}_t)^T\phi(\mathbf{x})] + \hat{\theta_0} \\ &= \sum_{t \in SV} \hat{\alpha_t}y_t [\phi(\mathbf{x}_t)^T\phi(\mathbf{x})] + \hat{\theta_0} \end{aligned}$$
によって新しいexample $\mathbf{x}$の推測$\hat{y}({\mathbf{x}})$が計算できる.
$\hat{\theta_0}$は$\hat{\alpha}$を求めた後で,
$$\forall i \in SV. \ y_i(\hat{\theta}^T \phi(\mathbf{x}_i)+\hat{\theta_0}) = y_i \sum_{t \in SV}\hat{\alpha_t}[\phi(\mathbf{x}_t)^T\phi(\mathbf{x}_i)]+y_i\hat{\theta_0}=1$$
を解くことで得られる.
この解のgeometric marginは$1/\|\hat{\theta}_0\|$で得られる.つまり
$$\hat{\gamma_{geom}} = \left( \sum_{i=1}^n \sum_{j=1}^n \hat{\alpha_i}\hat{\alpha_j}y_iy_j K(i,j) \right)^{-\frac{1}{2}}$$

geometric marginを最大にするようなkernelが最適なkernelと言えるが,定数倍によってgeometric marginもその分定数倍になるので,kernelの比較には正規化が必要である.

Kernel Optimization

kernelのあるパラメータを変えて,問題により適したkernelをつくることができる. パラメータの最適化には,cross-validationやgeneralization errorに関連した基準(marginなど)が用いられる.

MIT OCW, Machine Learning 08日目 カーネル

Rohit Singh, Tommi Jaakkola, and Ali Mohammad. 6.867 Machine Learning. Fall 2006. Massachusetts Institute of Technology: MIT OpenCourseWare, https://ocw.mit.edu. License: Creative Commons BY-NC-SA.

• • Lecture 6.
    • Active Learning (cont)
    • Non-linear Predictions, Kernels
  • Lecture 7.
    • Linear Regression and Kernels
    • Kernels

Lecture 6.

Active Learning (cont)

$y = \theta^{*}\mathbf{x} + \theta^*_0 + \epsilon, \ \ \ \epsilon \sim N(0,\sigma^2)$というlinear modelについて,最尤法で推測されるパラメータ$\hat{\theta}, \hat{\theta_0}$のMSEは
$$E\left[\left\|\left[\begin{array}{} \hat{\theta} \\ \hat{\theta_0} \end{array} \right] - \left[\begin{array}{} {\theta}^{*} \\ {\theta_0}^* \end{array} \right] \right\|^2 | \mathbf{X} \right] = \sigma^{*2} Tr[(\mathbf{X^TX})^{-1}]$$
となることから,$\mathbf{X}$をうまく設計することで少ないexampleからよりよい推測を行うことをactive learningといった. $\mathbf{X}$の設計で最も単純な方法は,$\mathbf{x_1}, ..., \mathbf{x_k}$があるときに,$Tr[\mathbf{X^TX}]$が最少になるように$\mathbf{x}_{k+1}$を選ぶという操作を繰り返すというのがある. すでに$\mathbf{X}$があって,$\mathbf{A}=(\mathbf{X^TX})^{-1}$とする. $[\mathbf{x}^T, 1]$を$\mathbf{X}$の行に新たに加えることを考える.
$$\left[\begin{array}{} \mathbf{X} \\ \mathbf{x}^T 1 \end{array} \right]^T\left[\begin{array}{} \mathbf{X} \\ \mathbf{x}^T 1 \end{array} \right] = (\mathbf{X^TX}) + \left[\begin{array}{} \mathbf{x} \\ 1 \end{array} \right]\left[\begin{array}{} \mathbf{x} \\ 1 \end{array} \right]^T = \mathbf{A}^{-1} + \mathbf{vv^T} \ \ \ (\mathbf{v}=[\mathbf{x}^T, 1]^T)$$
$$Tr[(\mathbf{A}^{-1} + \mathbf{vv^T})^{-1}]$$
を最小化する$\mathbf{v}$を考える.
$$(\mathbf{A}^{-1} + \mathbf{vv^T})^{-1} = \mathbf{A} - \frac{1}{1 + \mathbf{v^TAv}} \mathbf{Avv^TA}$$
であって,$Tr(A+B) = Tr(A)+Tr(B), Tr(AB)=Tr(BA)$を考えれば
$$Tr[(\mathbf{A}^{-1}+\mathbf{vv^T})^{-1}] = Tr[A] - \frac{\mathbf{v^T AAv}}{1 + \mathbf{v^TAv}}$$
が成立する. ($\mathbf{v^TAAv}$は実数で,traceはその実数そのもの)
任意の$\mathbf{v}$に$\frac{\mathbf{v^TAAv}}{1+\mathbf{v^TAv}}>$だから,どのような$\mathbf{x}$を加えたとしてもMSEは減少するが,減少量が最大であるような$\mathbf{x}$を求めたい.
$$\frac{\mathbf{v^TAAv}}{1+\mathbf{v^TAv}}$$
の大きさは$A$の最大の固有値が上限である. 言い換えると,新しいexampleによってパラメータ空間からせいぜい1つだけ自由度を減じることが出来る. $\mathbf{x}$に制限がなければ,$\mathbf{A}$の最大の固有値に対応する固有ベクトルに平行な長さ無限のベクトルを$\mathbf{v}$とするのだが,$\|\mathbf{v}\|\leq c$という制限が有る場合には,最大固有値に対応する固有ベクトルと平行でながさ$c$のベクトルを$\mathbf{v}$とする. ほかにも$\mathbf{x}$に制限が有る場合には,$\mathbf{v}$もその制限を考慮することになる.

これまでMSEを推定量の良さの基準としてきたが,今度はvarianceを考える.
$$\begin{aligned} var[y|\mathbf{x, X}] &= E\left[(\hat{\theta}^T\mathbf{x}+\hat{\theta}_0 - \theta^{*T}\mathbf{x} -\theta^{*}_0)^2 | \mathbf{x, X} \right]\\ &=E\left[\left[\begin{array}{} \mathbf{x} \\ 1 \end{array} \right]^T \left(\left[ \begin{array}{} \hat{\theta} \\ \hat{\theta_0} \end{array} \right] - \left[ \begin{array}{} {\theta}^* \\ {\theta_0}^* \end{array} \right]\right) \left(\left[ \begin{array}{} \hat{\theta} \\ \hat{\theta_0} \end{array} \right] - \left[ \begin{array}{} {\theta}^* \\ {\theta_0}^* \end{array} \right]\right)^T\left[\begin{array}{} \mathbf{x} \\ 1 \end{array} \right]| \mathbf{x, X}\right]\\ &= \left[\begin{array}{} \mathbf{x} \\ 1 \end{array} \right]^T \sigma^{*2}(\mathbf{X^TX})^{-1}\left[\begin{array}{} \mathbf{x} \\ 1 \end{array} \right] \\ &= \sigma^{*2}\cdot \mathbf{v^TAv}\end{aligned}$$

よって,$\mathbf{v^TAv}$が最大になるような$\mathbf{v}$がよいが,これはMSEを小さくするような$\mathbf{v}$と同じである.
(MSEを小さくしつつvarianceを小さくすることが対立することを言いたいのかと思ったら,varianceを大きくしたいらしい・・・)

Non-linear Predictions, Kernels

$\mathbf{x}$の非線形な写像に対する像$\phi(\mathbf{x})$に対してこれまで議論してきた方法が使える.例えば$y = \theta x + \theta_0 + \epsilon, \epsilon \sim N(0, \sigma^2)$というlinear modelが有るとき,$x$を$x^2$を含む高次元のベクトルに写像してquadratic(二次) modelが得られ,$x^3$を含む高次元のベクトルに写像するとthird order modelが得られる.
$\phi(x) = [1, \sqrt{2}x, x^2]^T, \phi(x)=[1, \sqrt{3}x, \sqrt{3}x^2, x^3]^T$のような感じである.$\sqrt{2}$や$\sqrt{3}$の意味は後で見る.
新しいpolynomial regression modelは
$$y = \theta^T \phi(x) + \theta_0 + \epsilon, \ \ \epsilon \sim N(0, \sigma^2)$$
となる. 高次元空間に写像してから線形回帰するわけだが,このときregularizationを行わないとoverfittingが起きることが多い.(figure 2)
!

$\mathbf{x}$が多次元の場合も,
$$\mathbf{x}=[x_1, x_2]^T\mapsto^{\phi} [1, x_1, x_2, \sqrt{2}x_1x_2, x_1^2,x_2^2]^T = \phi(\mathbf{x})$$
というふうにしてより高次元な空間に写像できる.
高次元な空間への変換は計算コストが膨大になることが有るが,$\phi$を直接計算せずとも,例えば
$$\begin{aligned} \phi(x) &= [1, \sqrt{3}x, \sqrt{3}x^2, x^3]^T \\ \phi(x') &= [1, \sqrt{3}x', \sqrt{3}x^{'2}, x^{'3}]^T \\ \phi(x)^T\phi(x') &= 1 + 3xx' + 3(xx')^2 + (xx')^3 = (1+xx')^3 \end{aligned}$$
のように,$\phi(x)^T\phi(x')=k(x,x')$と,$\phi$を暗黙に表現する計算が簡単な$K$が存在することが有る(存在するように$\phi$を定めたのである). $\phi$ではなく計算が簡単な$K$を使うように問題を書き換えることを考える.

Lecture 7.

Linear Regression and Kernels

$\theta_0$を外したモデル$y = \theta^T \phi(\mathbf{x}) + \epsilon$はの推測は
$$J(\theta) = \sum_{t=1}^n (y_t-\theta^T \phi(\mathbf{x}_t))^2 + \lambda\|\theta\|^2$$
の最適化問題である. 前節で述べたとおり,$\phi$ではなく$k$でこの最適化問題を表現する.
regularizationによって$\theta$は$0$に圧縮され,$\theta$のtraining feature vectorと関係ない次元は$0$になる. よってこの問題の解は$\{\phi(\mathbf{x}_t)\}$の張る空間の元である.
proof.

局地の条件を考えると
$$\frac{dJ}{d\theta} = -2 \sum_{t=1}^n \underline{(y_t-\theta^T\phi(\mathbf{x}_t))}_{\alpha_t}\phi(\mathbf{x}_t) + 2\lambda \theta=0$$
$$\theta = \frac{1}{\lambda} \sum_{t=1}^n \alpha_t \phi(\mathbf{x}_t)$$
は$\frac{dJ}{d\theta}=0$を満たして,最適解である.

$$\alpha_t = y_t - \theta^T \phi(\mathbf{x}_t)=y_t - \frac{1}{\lambda}\sum_{t'=1}^n \alpha_{t'} \phi(\mathbf{x_{t'}})^T \phi(\mathbf{x}_t)$$
が成立するから,$\alpha_t$は$y_t$と$\phi(\mathbf{x}), \phi(\mathbf{x'})$だけで決まる.
Gram行列
$$\mathbf{K} = \left[\begin{array}{} \phi(\mathbf{x}_1)^T\phi(\mathbf{x}_1) & \phi(\mathbf{x}_1)^T\phi(\mathbf{x}_2) & \cdots & \phi(\mathbf{x}_1)^T\phi(\mathbf{x}_n) \\ \cdots & \cdots & \cdots & \cdots \\ \phi(\mathbf{x}_n)^T\phi(\mathbf{x}_1) & \cdots & \cdots &\phi(\mathbf{x}_n)^T\phi(\mathbf{x}_n) \end{array} \right]$$
によってベクトルで書くと
$$\begin{aligned} \mathbf{a} &= [\alpha_1, ..., \alpha_n]^T \\ \mathbf{y} &= [y_1, ..., y_n]^T \\ \mathbf{a} &= \mathbf{y} - \frac{1}{\lambda} \mathbf{Ka} \end{aligned}$$
そして解は
$$\hat{\mathbf{a}} = \lambda(\lambda \mathbf{I} + K)^{-1} \mathbf{y}$$
$\hat{\alpha}_t$が得られたら,
$$y = \hat{\theta}^T \phi(\mathbf{x}) = \sum_{t=1}^n (\hat{\alpha_t}/\lambda)\phi(\mathbf{x}_{t'})^T\phi(\mathbf{x})=\sum_{t=1}^n\hat{\alpha}_tK(\mathbf{x_{t'}, x})$$
によって,新しいexample $\mathbf{x}$に対してresponseの推測$y$が計算できる.ここで$K(\mathbf{x_{t'}, x})$はkernel functionという.

Kernels

以上で, regularized linear regressionをkernel formに変形できた. kernel function $K$を変えることで,例えば任意の次数のpolynomial expansionが実現できるし,polynomial expansion以外の$\mathbf{x}$を高次元に写した像を使ったlinear regressionも実現できる.
実現される高次元への写像の種類によって$K$を分類することが有る.例えば
- Polynomial kernel

$$K(\mathbf{x', x})=(1 + \mathbf{x^Tx'})^p, \ \ p = 1,2,...$$
- Radial basis kernel
$$K(\mathbf{x', x}) = \exp \left(-\frac{\beta}{2}\|\mathbf{x}-\mathbf{x}'\|^2 \right), \ \ \beta>0$$

polynomial kernelは,$\mathbf{x}=[x_1,...,x_n]^T$を$(x_1+\cdots +x_n)^p$を二項展開したときの各項へと写す写像$\phi$を考えたときのkernel functionで, radial basis kernelは無限次元空間への写像のkernel functionである. radial basis functionは$\mathbf{x}$と$\mathbf{x'}$の近さを表していると考えることが出来る.